Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
Работать с выражениями.
Задавать простые типы данных.
Задавать данные множественного типа.
Задавать данные строкового типа.
Писать программные комментарии.
Задавать переменные и определять их тип.
Использовать константы различного типа.
Данные множественного типа
Данные множественного типа
Наборы (множества)
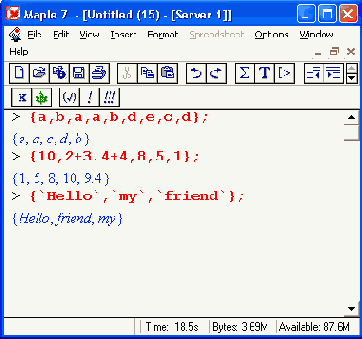
Любые выражения могут включаться также в наборы. Такие наборы в виде множеств создаются с помощью фигурных скобок { }:
Идентификация констант
Идентификация констант
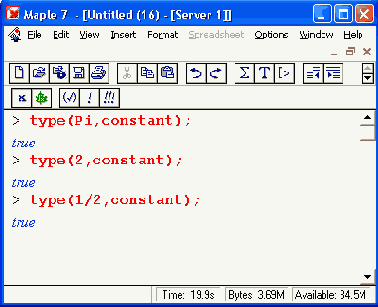
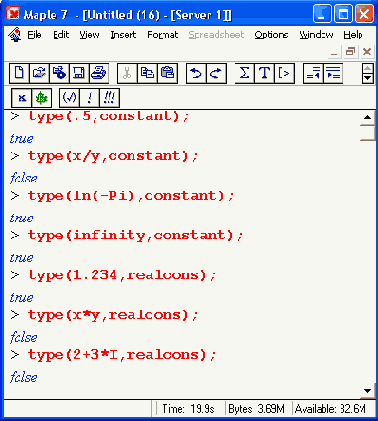
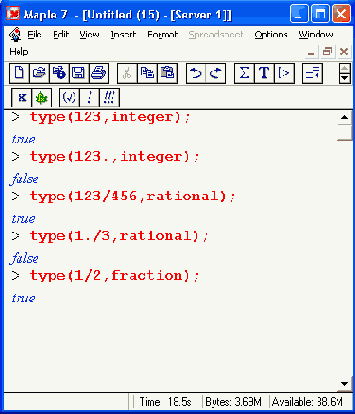
Функции type(х, constant) и type(x, realcons) возвращают логическое значение true, если х представляет целочисленную или вещественную константу, и false, если х не является константой. Таким образом, эти функции можно использовать для идентификации констант, например:
Идентификаторы (имена) переменных
Идентификаторы (имена) переменных
Переменные задаются своим именем — идентификатором, который должен начинаться с буквы и быть уникальным. Это значит, что ключевые слова языка Maple нельзя использовать в качестве имен переменных. Хотя имена ряда команд и функций можно использовать в качестве идентификаторов переменных, делать это крайне нежелательно. Ограничений на длину идентификатора практически нет — точнее, она не должна превышать 524 275 символов! Так что сложностей с подбором идентификаторов для переменных у вас не будет.
Имена переменных могут содержать одну букву (например, х, Y или Z) либо ряд букв (Xmin или Хmах). В любом случае имя переменной надо начинать с буквы. Некоторые символы, например знак _, могут использоваться в именах (например, Var_l, Var_2). Нельзя, однако, вводить в имена переменных знаки, обозначающие операторы, — например, а/b или а-b будет истолковано как деление а на b или вычитание из переменной а переменной b.
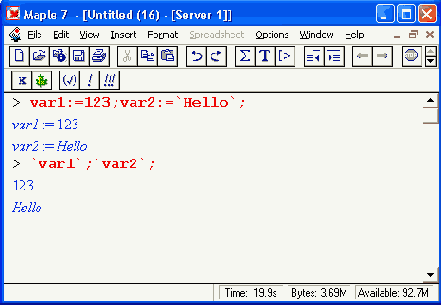
Имена могут задаваться в обратных апострофах. При этом они просто тождественны именам без апострофов:
Комплексные числа
Комплексные числа
Maple 7, естественно, может работать с комплексными числами. Мнимая единица в комплексном числе (корень квадратный из -1) обозначается как I. Функции Re(x) и Im(x) возвращают действительную и мнимую части комплексных чисел. Примеры задания комплексного числа и вывода его действительной и мнимой частей представлены ниже:
Константы
Константы
Числовые константы
Константы - это простейшие именованные объекты, несущие заранее предопределенные значения. Их имена (идентификаторы) также заранее определены и не могут меняться. Подробную информацию о константах можно найти, исполнив команду ?constant.
Обычные числовые константы не имеют имени и представлены просто числами, типы которых были указаны выше. Можно считать, что именем такой константы является само ее значение. Например, в выражении 2*sin(1.25) числа 2 и 1.25 являются числовыми константами. При этом указание десятичной точки делает константу действительным числом — например, 2 — это целочисленная константа, а 2., 2.0 или 1.25 — это уже действительные константы.
Контроль за числами
Контроль за числами
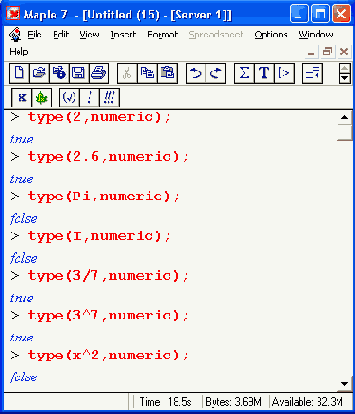
Числа могут служить объектами ввода, вывода и константами, входящими в математические выражения. Функция type(x, numeric) позволяет выяснить, является ли х числом. Если является, то она возвращает логическое значение true (истина), а если нет, то false (ложь). Например:
Mapleязык и его синтаксис
Maple-язык и его синтаксис
Знаки алфавита
Язык Maple (или Maple-язык) является одновременно входным языком общения с Maple 7 и языком ее программирования. Входящие в него средства (прежде всего операторы и функции) подобраны настолько полно и удачно, что при решении подавляющего большинства типовых математических задач от пользователя не требуется знаний даже основ программирования. Для решения нужной задачи обычно достаточно составить алгоритм и подобрать набор нужных для его реализации функций и иных средств Maple-языка.
В то же время Maple-язык — один из самых мощных языков программирования математических задач, содержащий почти 3000 операторов, команд и функций, входящих в ядро, основную библиотеку и пакеты функций Maple 7. При этом относящаяся к традиционному программированию часть Maple-языка реализована с помощью довольно скромного набора специальных знаков и зарезервированных слов.
Большинство функций Maple 7 (в частности, все, входящие в пакеты) написаны на этом языке. Поэтому знание этого языка является определяющим в серьезном изучении Maple. Ниже Maple-язык описывается как типичный язык программирования.
Алфавит Maple-языка содержит 26 малых латинских букв (от а до z), 26 больших латинских букв (от А до Z), 10 арабских цифр (от 0 до 9) и 32 специальных символа (арифметические операторы +, -, *, /, знак возведения в степень ж и др.). Все они будут рассмотрены в данной главе. Имеется пять пар альтернативных символов (означающих одно и тоже):
"и** [ и (| ] и |) { и (* } и *)
К специальным одиночным и составным знакам относятся элементы синтаксиса языка:
Комментарии в программе, не выводимые в ячейки вывода, задаются после символа #. В них допустимо использовать все символы кодовых таблиц, что важно при вводе русскоязычных комментариев, использующих символы кириллицы. Применение последних для идентификаторов (имен) объектов недопустимо.
Массивы векторы и матрицы
Массивы, векторы и матрицы
Как отмечалось, важным типом данных являются списки (lists). Они создаются с помощью квадратных скобок, например:
[1,2,3,4] — список из четырех целых чисел;[1. ,2.34,5] — список из двух вещественных и одного целого числа;
[а,b.'Привет'] — список из двух символов (переменных) и строковой константы;
[sin(x), 2*cos(x) ,a^2-b] — список из трех математических выражений.
Для создания векторов (одномерных массивов) и матриц (двумерных массивов) служит функция array. Обычно она используется в следующих формах:
аrrау[а. .b,sl] — возвращает вектор с индексами от а до b и значениями в одномерном списке si;аrrау[а. .b,c. .d,s2] — возвращает матрицу с номерами строк от а до b, номерами столбцов от с до d и значениями в двумерном списке s2.
Неисполняемые программные комментарии
Неисполняемые программные комментарии
Часто возникает необходимость в задании программных комментариев. Любой текст после знака # рассматривается как невыводимый (неисполняемый) программный комментарий — даже если это математическое выражение. При этом он не вычисляется. Например:
> 2+3;#Это прииер. А это выражение не вычисляется: 4+5
.5
Комментарии полезны в программах на Maple-языке и обычно используются для объяснения особенностей реализованных алгоритмов.
Оценивание выражений
Оценивание выражений
Встречая выражение, Maple 7 оценивает его, то есть устанавливает возможность его вычисления. Если выражение — скалярная переменная, то ее значение будет выведено в ячейке вывода. Для переменных более сложных типов выводится не их значение, а просто повторяется имя переменной. Просто повторяются также имена неопределенных переменных.
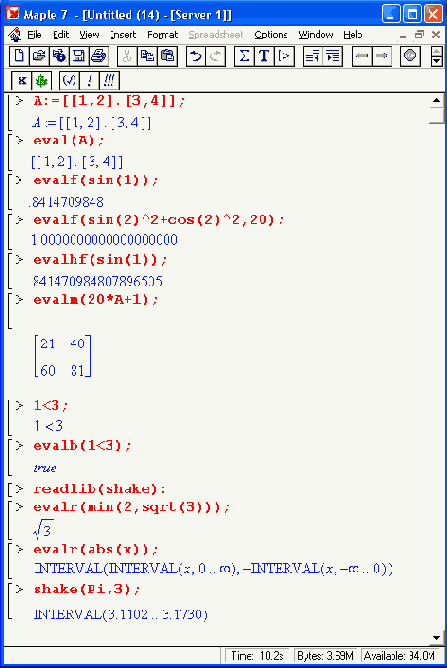
Для оценивания выражений различного типа существует группа функций, основные из которых перечислены ниже:
eval (array) — возвращает вычисленное содержимое массива array;evalf(expr, n) — вычисляет ехрr и возвращает вычисленное значение в форме числа с плавающей точкой, имеющего n цифр после десятичной точки;
eval hf(ехрг) — вычисляет ехрг и возвращает вычисленное значение с точностью, присущей оборудованию данного компьютера;
evalf(int(f, x=a..b)) — оценивает и возвращает значение определенного интеграла int(f,x=a. .b);
evalf(Int(f, x=a..b)) — оценивает и возвращает значение определенного интеграла, заданного инертной функцией Int(f,x=a. .b);
evalf(Int(f. x=a..b, digits, flag)) — аналогично предыдущему, но возвращает значение интеграла с заданным параметром digits числом цифр после десятичной точки и со спецификацией метода вычислений flag;
evalm(mexpr) — вычисляет значение матричного выражения mexpr и возвращает его;
evalb(bexpr) — вычисляет и возвращает значения логических условий; evalc(cexpr) — вычисляет значение комплексного выражения;
evalr (ехрr, ampl) — оценивает и возвращает значения интервальных выражений (функция должна вызываться из библиотеки);
shake(expr, ampl) — вычисляет интервальное выражение.
Для функции evalf параметр n является необязательным, при его отсутствии полагается n=10, то есть вещественные числа выводятся с мантиссой, имеющей десять цифр после десятичной запятой.
В выражении ехрr могут использоваться константы, например Pi, exp(l), и функции, такие как ехр, 1 n, arctan, cosh, GAMMA и erf. В матричном выражении mexpr для функции evalr могут использоваться операнды в виде матриц и матричные операторы &*, +, - и ^. В комплексных выражениях mexpr наряду с комплексными операндами вида (а + I*b) могут использоваться многие обычные математические функции:
| sin |
cos |
tan |
CSC |
sec |
cot |
| sinh |
cosh |
tanh |
csch |
sech |
coth |
| arcsin |
arccos |
arctan |
arccsc |
arcsec |
arccot |
| arcsinh |
arccosh |
arctanh |
arccsch |
arcsech |
arccoth |
| exp |
In |
•sqrt |
* |
abs |
conjugate |
| polar |
argument |
signura |
csgn |
Re |
Im |
| Ei |
LambertW |
dilog |
surd |
|
|
Примеры применения функций оценивания даны ниже:
Отмена операции присваивания и команда restart
Отмена операции присваивания и команда restart
Переменная, имеющая какое-либо значение, занимает в памяти намного больше места, чем неопределенная переменная. У последней место в памяти занимают только символы идентификатора. Поэтому нередко целесообразно отменить присваивание у тех переменных, которые в дальнейшем можно не использовать. Это может понадобиться и в том случае, когда какую-либо переменную с численным или иным значением нужно использовать просто как неопределенную переменную. Рассмотрим следующий пример:
Переменные
Переменные
Типы переменных
Как следует из самого названия, переменные — это объекты, значения которых могут меняться по ходу выполнения документа. Пока мы рассматриваем лишь глобальные переменные, доступные для модификации значений в любом месте документа. Тип переменной в системе Maple 7 определяется присвоенным ей значением — это могут быть целочисленные (integer), рациональные (rational), вещественные (real), комплексные (complex) или строчные (string) переменные и т. д. Переменные могут также быть символьного типа (их значением является математическое выражение) или типа списка (см. далее). Для явного указания типа переменных используется конструкция:
name::type
где name — имя (идентификатор) переменной, type — тип переменной, например целочисленный (integer), вещественный с плавающей точкой (float), с неотрицательным значением (nonneg), комплексный (complex) и т. д.
Последовательности выражений
Последовательности выражений
Maple 7 может работать не только с одиночными выражениями, но и с последовательностями выражений. Последовательность выражений — это ряд выражений, разделенных запятыми и завершенных фиксатором:
Преобразования чисел с разным основанием
Преобразования чисел с разным основанием
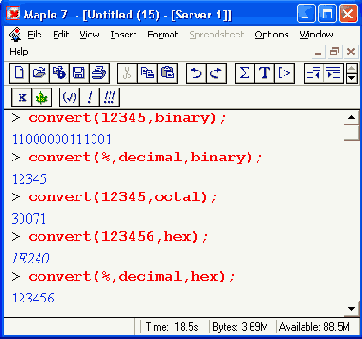
В Maple возможна работа с числами, имеющими различное основание (base), в частности с двоичными числами (основание 2 — binary), восьмеричными (основание 8 — octal) и шестнадцатеричными (основание 16 — hex). Функция convert позволяет легко преобразовывать форматы чисел:
Придание переменным статуса предполагаемых
Придание переменным статуса предполагаемых
В большинстве расчетов пользователей Maple вполне удовлетворяет статус переменных, соответствующий присвоенным им значениям. Однако серьезные расчеты предполагают, что переменные могут иметь определенные ограничения — например, они не должны принимать отрицательных значений при обычном вычислении квадратного корня или логарифма числа.
Для придания переменным статуса предполагаемых используется функция assume: assume(x.prop): где х — переменная, имя или выражение, prop — свойство. Следующие примеры показывают применение функции assume:
Присваивание переменным значений
Присваивание переменным значений
Поскольку Maple 7 прежде всего система символьной математики, то по умолчанию любые переменные рассматриваются как объекты символьного типа. Благодаря этому такие переменные могут фигурировать в математических выражениях (таких, как sia(x)/x) без их предварительного объявления. В отличие от обычных языков программирования такое использование переменных не влечет за собой появления сообщений об ошибках и является более естественным. Для присваивания переменным конкретных значений используется комбинированный символ присваивания «:=», например:
n:=1 — переменной n присваивается, целочисленное значение 1; х:=123.456 - переменной х присваивается вещественное значение 123.456; у:=17/19 — переменной у присваивается рациональное значение 17/18; name:='Piter' — переменной name присваивается строковое значение "Piter"; expr:=2*Pi/3 — переменной ехрг присваивается значение выражения 2л/3; V:=[1.2,3] - переменной V присваивается значение списка чисел [1,2,3]; М:=[[1,2.3].[4,5.б]] - переменной М присваивается значение двумерного массива; f :=х->х^2 - переменной f присваивается значение функции пользователя f(x)=x^2. Правая часть выражения присваивания определяет тип переменной. Например, она может быть целочисленной, действительной, строковой, индексированной (элемент массива) и т. д.
Простые типы данных
Простые типы данных
Числа и числовые константы
Maple 7 работает с числами следующего типа: целыми (О, 1, 123, -456 и т. д.), рациональными в виде отношения целых чисел (7/9, -123/127 и т. д.), вещественными с мантиссой и порядком (1.23Е5, 123.4567Е-10). Признаком вещественного числа является десятичная точка (запятая). Примеры простых операций с числами приведены ниже:
Помимо приведенных вариантов функция convert
Шаг 1
автоматическое устранение из них повторяющихся
Шаг 1
показывает применение этих средств
Шаг 1
Представление множества чисел на плоскости
Шаг 1
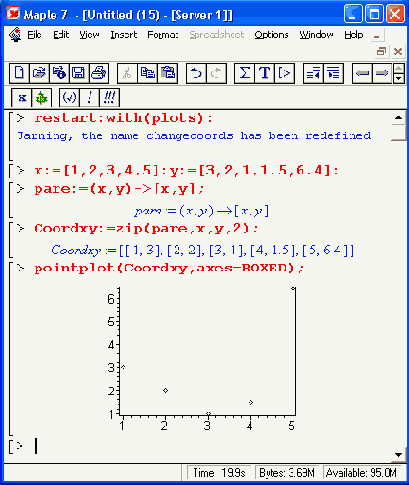
Рисунок 5.2. Представление множества чисел на плоскости
Двумерные списки часто путают с матрицами. Следует помнить, что векторы и матрицы создаются с помощью функции array и являются отдельным типом данных. Элементами векторов и массивов могут быть константы, переменные, выражения, списки и иные объекты. Эти элементы являются индексированными переменными и их положение указывается индексами. Имеется множество функций для работы со списками, массивами и матрицами. Они будут рассмотрены в дальнейшем. В принципе, размерность массивов, создаваемых списками, не ограничена и массивы могут быть многомерными.
Пустая таблица резервирует память под
Шаг 1
Шаг 1
Шаг 1
о такой экзотической возможности, как
Шаг 1
в идентификаторах различаются, так что
Шаг 1
Для проверки предполагаемого имени на уникальность достаточно выполнить команду ?name, где name — выбранное имя. Если при этом откроется окно справки с этим именем, значит, оно уже использовано в Maple. Лучше воздержаться от его применения, так как связанная с этим именем команда или функция перестает работать, как только это имя закрепляется за какой-либо переменной.
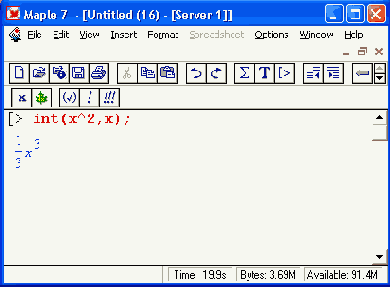
Здесь не удалось вычислить интеграл
Шаг 1
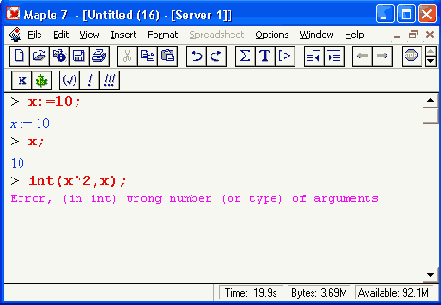
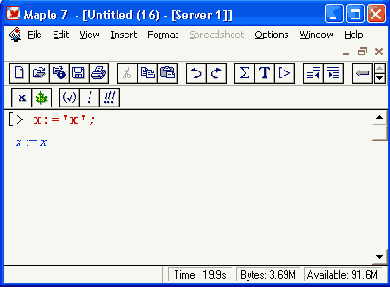
Для отмены присваивания надо использовать следующее выражение:
и при выводе сопровождается знаком
Шаг 1
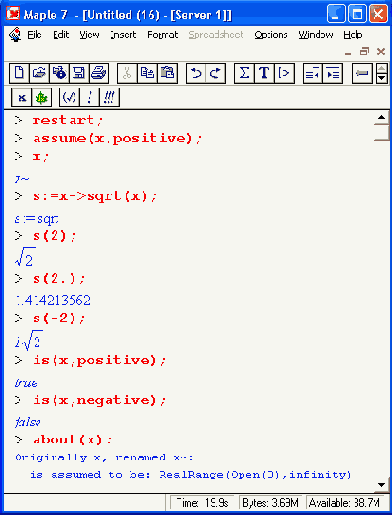
Иногда к уже имеющимся признакам надо добавить новые. Для этого используется функция additionally:
и вычисления математических выражений более
Шаг 1
Для выполнения любых математических операций необходимо обеспечить ввод в систему исходных данных — в общем случае математических выражений. Для ввода их и текстовых комментариев служат два соответствующих типа строк ввода. Переключение типа текущей строки ввода осуществляется клавишей F5. Строка ввода математических выражений имеет отличительный символ >, а строка ввода текстов такого признака не имеет.
В строке ввода может располагаться несколько выражений. Фиксаторами (указанием, что выражение окончено) их могут быть символы ; (точка с запятой) и : (двоеточие). Символ «:» фиксирует выражение и задает вывод результатов его вычисления. А символ «:» фиксирует выражение и блокирует вывод результатов его вычисления. Фиксаторы выполняют также функцию разделителей выражений, если в одной строке их несколько.
Ввод выражения оканчивается нажатием клавиши Enter. При этом маркер ввода (жирная мигающая вертикальная черта) может быть в любой позиции строки. Если надо перенести ввод на новую строку, следует нажимать клавиши Shift и Enter совместно. С помощью одного, двух или трех знаков % (в реализациях до Maple V R5 это был знак прямых кавычек ") можно вызывать первое, второе или третье выражение с конца сессии:
В дальнейшем мы многократно будем
Шаг 1
Для автоматического формирования последовательности выражений
Шаг 1
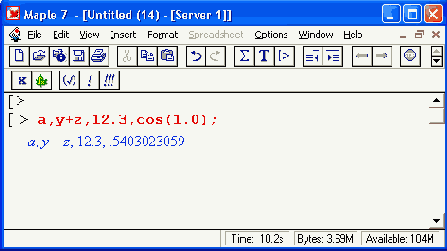
Шаг 1
Шаг 1
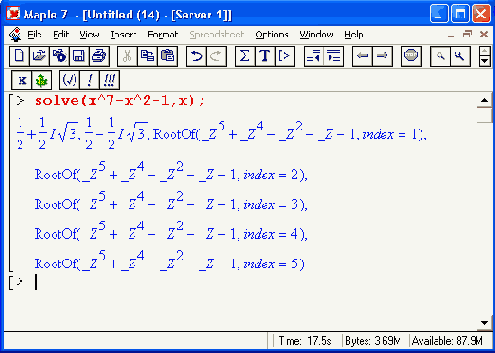
Как видно из этих примеров,
Шаг 1
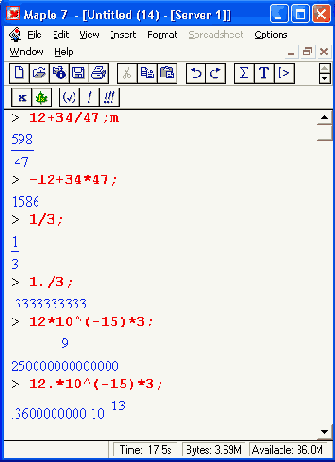
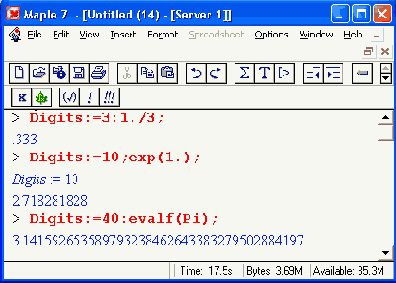
для отделения целой части мантиссы от дробной используется разделительная точка; нулевая мантисса не отображается (число начинается с разделительной точки); мантисса отделятся от порядка пробелом, который рассматривается как знак умножения; мнимая часть комплексных чисел задается умножением ее на символ мнимой единицы I (квадратный корень из -1). Десятичная точка в числах имеет особый статус — указание ее в любом месте числа, даже в конце, делает число вещественным и ведет к переводу вычислений в режим работы с вещественными числами. При этом количеством выводимых после десятичной точки цифр можно управлять, задавая значение системной переменной окружения Digits:
Комплексные числа обычно представляют на
Шаг 1
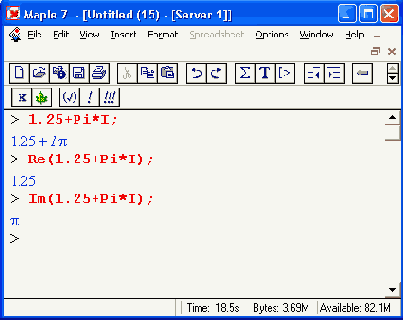
Окружность радиуса abs(z)=sqrt(a2 + b2) представляет абсолютное значение комплексного числа z=a+b*I. Она является геометрическим множеством комплексных чисел, образованных концом вращающегося радиус-вектора числа z вокруг его начала в точке (0, 0) комплексной плоскости. Позже мы рассмотрим ряд функций для работы с комплексными числами.
можно использовать для проверки того,
Шаг 1
В конце приведенных примеров показано,
Шаг 2
Шаг 2
Шаг 2
в прямые апострофы ликвидирует присваивание.
Шаг 2
а вначале задан признак положительности,
Шаг 2
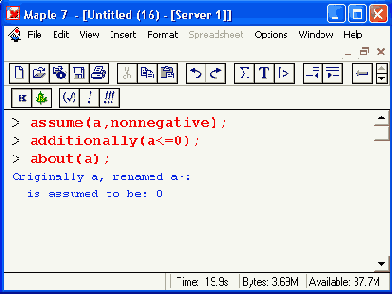
Предполагаемую переменную можно также изменить путем присваивания ей нового значения, противоречащего ее статусу:
Особая роль при вводе выражений
Шаг 2
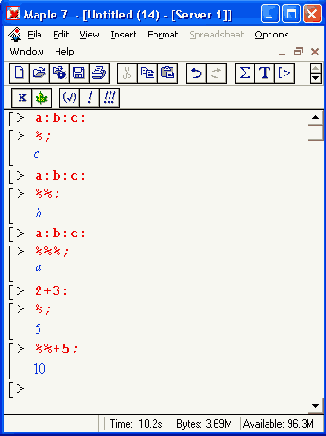
Для создания последовательностей выражений можно
Шаг 2
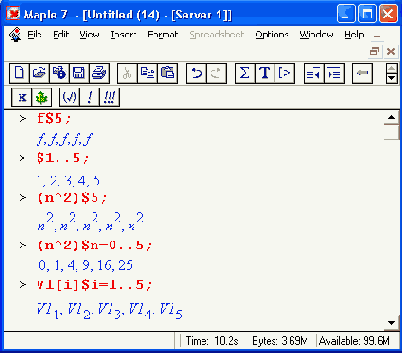
для отметки предполагаемых переменных, постоянные
Шаг 2
имеет множество функций. Они
Шаг 2
Шаг 2
Шаг 2
они демонстрируют замену функции косинуса
Шаг 3
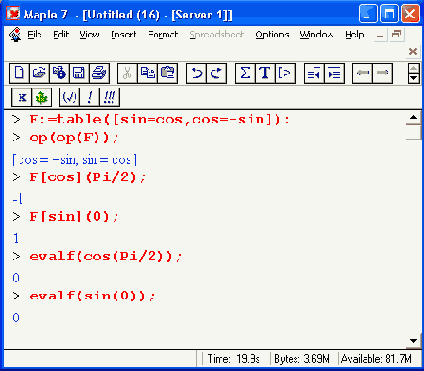
с помощью выражения вида
Шаг 3
Для отмены переменным статуса предполагаемых
Шаг 3
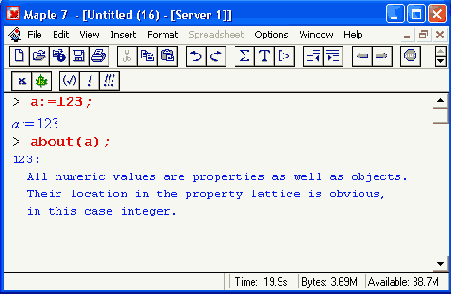
Некоторые другие возможности обрамления выражений
Шаг 3
Для завершения работы с текущим документом достаточно исполнить команду quit, done или stop, набранную в строке ввода (со знаком ; в конце).
Шаг 3
Шаг 3
и комплексных чисел на плоскости
Шаг 3
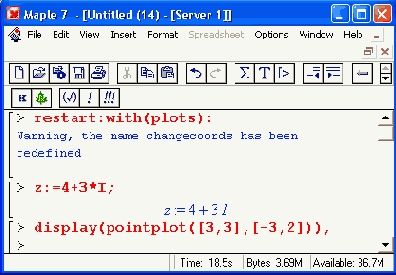
Рисунок 5.1. Представление обычных и комплексных чисел на плоскости
Для представления чисел на Рисунок 5.1 используется функция pointplot(list), где list — список координат точек. Эта функция становится доступной при подключении пакета plots командой with(plots). Кроме того, использована функция вывода ряда графических объектов на один график — display (см. далее описание представления комплексных чисел).
С помощью функции convert Maple 7 может преобразовывать числа с различным основанием (от 2 до 36, в том числе бинарные и шестнадцатеричные) в десятичные числа:
Шаг 3
Шаг 3
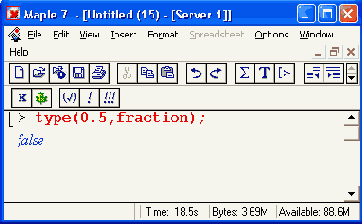
Для отмены присваивания значений разом
Шаг 4
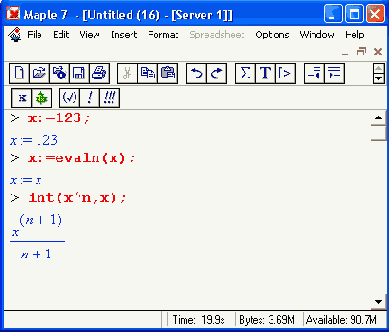
реализует точную арифметику. Это
Шаг 4
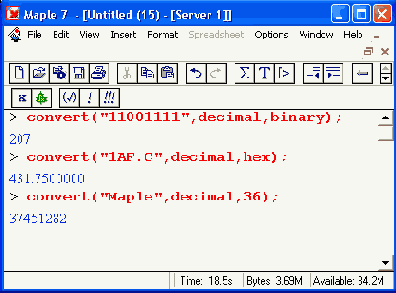
Следует отметить, что команда restart
Шаг 5
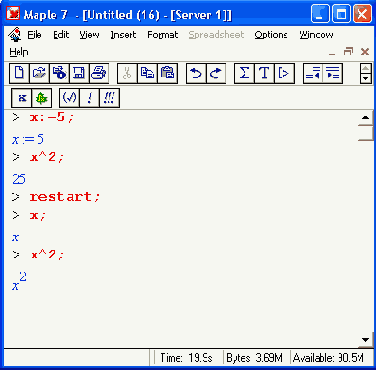
Важно отметить, что Maple сохраняет в памяти все определения и присваивания, которые были сделаны во всех загруженных в систему документах. Поэтому результаты вычислений в текущем документе могут зависеть от определений в других документах. Команда restart позволяет исключить эту зависимость.
Шаг 5
Шаг 5
Списки выражений
Списки выражений
Для создания упорядоченных наборов — списков — служат квадратные скобки [ ]:
> [10,2+3.4+4,8,5,1]: [10,5,8,8,5,1]
Как нетрудно заметить, элементы списков преобразуются и выводятся строго в том порядке, в каком они были заданы. Списки широко применяются для задания векторов и матриц.
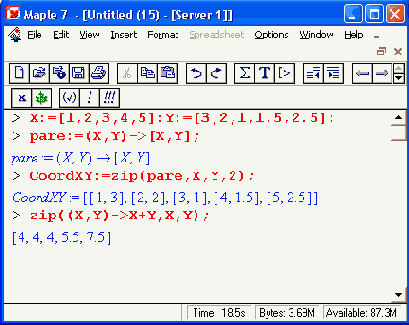
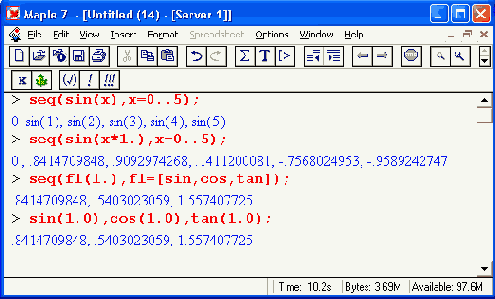
В ряде случаев, например при подготовке данных для двумерных графиков, возникает необходимость в подготовке парных списков — скажем, координат точек (х, у) графика. Для этого можно использовать функцию zip(f, u, v) или zip(f, u, v, d). Здесь f — бинарная функция, u, v — списки или векторы, d — необязательное значение. Примеры применения функции zip даны ниже:
Строки и комментарии
Строки и комментарии
Строковые данные
Строки как тип данных — это просто цепочки символов. Они обычно используются для создания текстовых комментариев. Строки должны каким-либо образом выделяться, чтобы Maple не отождествляла их с именами констант и переменных. Для этого строки-комментарии имеют внутренний разделительный признак, который устанавливается при их вводе (нажатием клавиши F5, которое приводит к исчезновению знака >).
В других случаях последовательность символов рассматривается как строка, если она заключена в обратные апострофы, то есть в знаки '. Два апострофа подряд формируют апостроф как знак символьной строки, например `abc``def ` дает строку abc`def. Любое математическое выражение может входить в строку, разумеется, оно при этом не выполняется:
> '2+2 не всегда "четыре"';
2+2 не всегда 'четыре'
Строковые константы
Строковые константы
Строковыми константами являются произвольные цепочки символов, заключенные в обратные апострофы, например 'Hello', 'Привет', 'My number' и т. д. Числа, заключенные в апострофы, например '123456', также становятся строковыми константами, которые нельзя использовать в арифметических выражениях. Строковые константы представляют значения строковых переменных. В них можно использовать символы кириллицы при условии, что соответствующий шрифт имеется.
Таблицы
Таблицы
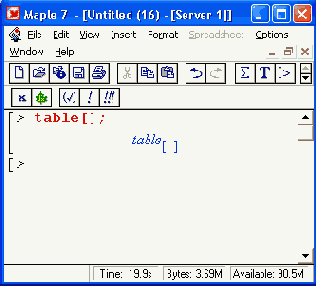
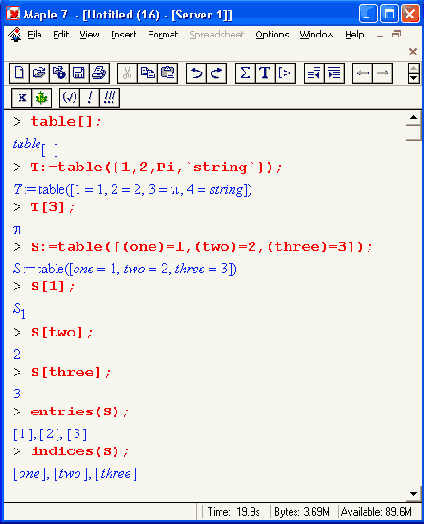
Еще одним важным типом множественных данных являются таблицы. Они задают данные с произвольной индексацией. Для создания таблиц служит функция table, которая при вызове в простейшем виде table[] создает шаблон пустой таблицы:
Встроенные в ядро константы
Встроенные в ядро константы
Есть также ряд констант, которые правильнее считать заведомо определенными глобальными переменными:
false — логическое значение «ложно»;gamma — константа Эйлера, равная 0.5772156649...;
infinity — положительная бесконечность (отрицательная задается как infinity);
true — логическое значение «истинно»;
Catalan — константа Каталана, равная 0.915965594...;
FAIL — специальная константа (см. справку, выдаваемую по команде ?FAIL);
I — мнимая единица (квадратный корень из -1);
Pi — представляет константу = 3.141...
Любопытно, что в этот список не входит основание натурального логарифма — число е. В качестве этой константы рекомендуется использовать ехр(1). Она отображается как жирная прямая буква Е. A exp(l.0) выводит 2.71828... (что и следовало ожидать).
Выражения и основы работы с ними
Выражения и основы работы с ними
Выражения и их ввод
Фактически Maple 7 — это система для манипулирования математическими выражениями.
Выражение в системе Maple — это объект, вполне соответствующий сути обычного математического выражения. Оно может содержать операторы, операнды и функции с параметрами. В этом уроке выражения записываются на Maple-языке без использования специальных средств для их представления в естественном математическом виде. Благодаря этому запись выражений и приводимых примеров одинаково пригодна для любой реализации системы Maple — даже под MS-DOS. Такая запись получается наиболее короткой, ее можно выводить и распечатывать без применения графических средств. Кроме того, она соответствует виду, принятому в справочной системе Maple.
Однако пользовательский интерфейс системы Maple 7 для Windows позволяет представлять как вводимые, так и выводимые выражения в самых различных формах, в том числе в естественном математическом виде — примеры этого многократно приводились и будут приводиться в дальнейшем. Maple 7 имеет многочисленные функции преобразования форматов, позволяющие менять форму представления данных.
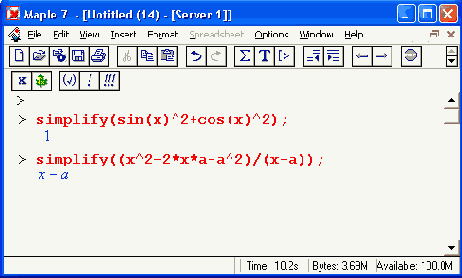
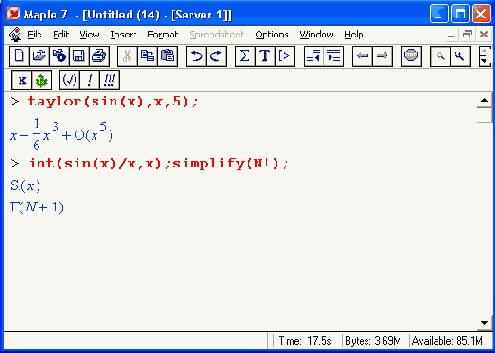
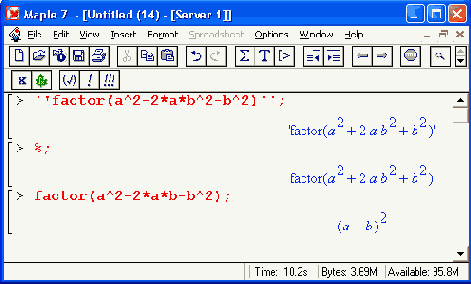
Выражения в Maple могут оцениваться и изменяться в соответствии с заданными математическими законами и правилами преобразований. Например, функция упрощения выражений simplify способна упрощать многие математические выражения, записанные в качестве ее параметра (в круглых скобках):
Вывод выражений
Вывод выражений
При выполнении порой даже простых операций результаты получаются чрезвычайно громоздкими. Для повышения наглядности выражений Maple 7 выводит их с выделением общих частей выражений и с присваиванием им соответствующих меток. Метки представлены символами #N, где N — номер метки. Помимо меток при выводе результатов вычислений могут появляться и другие специальные объекты вывода, например корни RootOf, члены вида О(х"), учитывающие погрешность при разложении функций в ряд, и обозначения различных специальных функций, таких как интегральный синус, гамма-функция и др. Примеры такого вывода приведены ниже:
Зарезервированные слова
Зарезервированные слова
Зарезервированные слова используются для создания условных выражений, циклов, процедур и управляющих команд. Список 42 зарезервированных слов Maple 7 дан ниже.
| and |
break |
by |
catch |
description |
| do |
done |
el if |
else |
end |
| error |
export |
fi |
finally |
for |
| from |
global |
if |
in |
intersect |
| local |
minus |
mod |
module |
next |
| not |
od |
option |
options |
or |
| proc |
quit |
read |
return |
save |
| stop |
then |
to |
try |
union |
| use |
while |
|
|
|
Совокупность правил, по которым записываются определения всех объектов Maple-языка, называется его синтаксисом. Некоторые особенности синтаксиса полезно знать уже в начале освоения Maple. Например, то что знак - (минус) имеет двойное значение. Применительно к одному числу, переменной или выражению он меняет их знак. Однако два знака минус подряд (например, в записи --3) задавать нельзя. Другое назначение знака минус — создание операции вычитания, например 5-2 или а-b. Соответственно двойное назначение имеет и знак •+, причем число без знака считается положительным, так что +5=5.
При вводе действительных чисел с порядком для указания порядка используется символ * (например, 2*1(Г100 или 2*1(Г-100). Для возведения числа в степень наряду с оператором *• можно использовать и составной оператор ** (две звездочки подряд). Для изменения общепринятого приоритета вычислений используются круглые скобки, в них же задаются параметры функций и процедур. Более подробно синтаксис Maple-языка рассматривается ниже.
Некоторые операторы представлены двумя символами — например, оператор присваивания переменным их значения := содержит двоеточие и знак равенства. В таких операторах между символами недопустим знак пробела. Однако его можно использовать между отдельными частями выражений — так, (а+b)/с эквивалентно (а + b) / с.
По набору операторов и функций Maple-язык намного превосходит любой универсальный язык программирования. Это позволяет наряду с обычными программными конструкциями задавать множество специальных конструкций, подчас резко упрощающих запись математических выражений. К примеру, возможна работа со списками имен функций. Язык Maple имеет множество операций над символьными выражениями и гибкий аппарат создания и преобразования типов данных и результатов вычислений.
Для большинства пользователей возможности языка Maple кажутся явно избыточными, и большинство наиболее распространенных операций в нем реализуется несколькими способами. Однако каждый пользователь волен выбирать из множества возможностей именно те, которые ему необходимы в конкретной предметной области. Поскольку таких областей превеликое множество, то обширные возможности Maple лишними не являются.
Защита идентификаторов констант
Защита идентификаторов констант
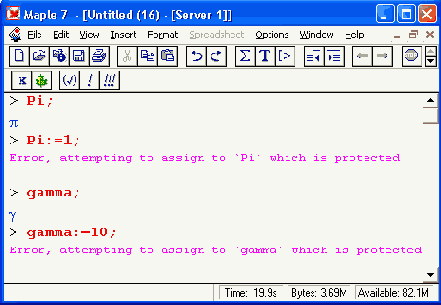
Имена встроенных констант (как и имена функций) защищены специальным атрибутом protected. Поэтому (без его снятия) константам нельзя присваивать какие-либо значения:
