Что нового мы узнали?

В этом уроке мы научились:

Осуществлять основные операции с выражениями. Выполнять приложения и подстановки. Упрощать и расширять выражения. Осуществлять факторизацию выражений. Выполнять комплектование выражений по степеням. Программировать некоторые символьные операции.

Факторизация выражений

Разложение целых и рациональных чисел

Для разложения целых или рациональных чисел на множители в виде простых чисел служит функция:

ifactor(n)

или

ifactor(n,method)

где n — число, method — параметр, задающий метод разложения. Другая библиотечная функция, if actors(n), возвращает результат разложения в форме вложенных списков:

Функции сортировки и селекции

Сортировка и селекция выражений широко используются в практике символьных преобразований. Для выполнения сортировки служит функция sort, применяемая в одной из следующих форм:

sort(L) sort(L. F) sort(A) sort(A. V)

Здесь L — список сортируемых значений, F — необязательная булева процедура с двумя аргументами, А — алгебраическое выражение, V — необязательные дополнительные переменные.

Функциональные преобразования элементов списков

Еще две функции, реализующие операции подстановки, указаны ниже:

map(fcn, expr. arg2. .... argn)

map2(fcn, argl, expr. arg3, .... argn)

Здесь fen — процедура или имя, expr — любое выражение, argi — необязательные дополнительные аргументы для fen.

Первая из этих функций позволяет приложить fen к операндам выражения ехрr. Приведенные далее примеры иллюстрируют использование функции mар.

Комплектование по степеням

Еще одна функция общего назначения — collect — служит для комплектования выражения ехрr по степеням указанного фрагмента х (в том числе множества либо списка). Она задается в одной из следующих форм:

collect(a. x)

collect(a. x. form, func)

Во второй форме этой функции дополнительно задаются параметры form (форма) и func (функция или процедура). Параметр form может иметь два значения- recursive (рекурсивная форма) и distributed (дистрибутивная форма). Параметр func позволяет задать имя функции, по которой будет идти комплектование ехрr. Примеры применения функции collect представлены ниже:

Контроль за типами объектов

Выражения и их части в Maple 7 рассматриваются как объекты. В ходе манипуляций с ними важное значение имеет контроль за типом объектов. Одной из основных функций, обеспечивающих такой контроль, является функция whattype(object), возвращающая тип объекта, например string, integer, float, fraction, function и т. д. Могут также возвращаться данные об операторах. Примеры применения этой функции даны ниже:

> whattype(2+3);

integer

> whattype(Pi):

symbol

> whattype(123./5)

float

> whattype(l/3i:

fraction

> whattype(sin(x));

function

> whattype([1.2.3,a,b,c])

;list

> whattype(a+b+c);

> whattype(a*b/c):

> whattype(a'b):

> whattype(H-2+3=4);

С помощью функции type(object.t) можно выяснить, относится ли указанный объект к соответствующему типу t, например:

> type(2+3,integer):

true

> type(s1n(x).function);

true

> typeChello,string);

false

> type("hello",string);

true

> typed/3.fraction):

true

При успешном соответствии типа объекта указанному (второй параметр) функция type возвращает логическое значение true, в противном случае — false.

Для более детального анализа объектов может использоваться функция hastype(expr. t), где ехрr — любое выражение и t — наименование типа подобъекта.

Эта функция возвращает логическое значение true, если подобъект указанного типа содержится в выражении ехрr. Примеры применения этой функции даны ниже:

> hastype(2+3,integer);

true

> hastype(2+3/4.integer):

false

> hastype(2*sin(x).function);

true

> hastype(a+b-c/d,'+'):

true

Еще одна функция — has(f.x) — возвращает логическое значение true, если подобъект х содержится в объекте f, и false в ином случае:

> has(2*sin(x),2);

true

> has(2*sin(x).V);

false

> has(2*sin(x),3-l);

true

Следует отметить, что соответствие подобъекта выражения указанному подобъекту понимается в математическом смысле. Так, в последнем примере подобъект «3 - 1», если понимать его буквально, в выражении 2*sin(r) не содержится, но Maple-язык учитывает соответствие 3 - 1 = 2, и потому функция has в последнем примере возвращает true.

Основные операции с выражениями

Работа с частями выражений

Выражения (ехрr) или уравнения (eqn) обычно используются как сами по себе, так и в виде равенств или неравенств. В последнем случае объекты с выражениями имеют левую и правую части. Для простейших манипуляций с выражениями полезны следующие функции:

cost (а) — возвращает число сложений и умножений в выражении а (функция пакета codegen); Ihs(eqn) — выделяет левую часть eqn; rhs(eqn) — выделяет правую часть eqn; normal (ехрr) — дает нормализацию (сокращение) ехрr в виде дроби; numer(expr) — выделяет числитель ехрr; Оdenom(expr) — выделяет знаменатель ехрr.

Ввиду очевидности действия этих функций ограничимся наглядными примерами их применения:

@@...

abs

arctan

conjugate

exp

piecewise

polylog

power

product

radical

range

signum

trig

Примеры применения функции combine представлены ниже:

Подстановки

Функциональные преобразования подвыражений

Нередко бывает необходимо заменить некоторое подвыражение в заданном выражении на функцию от этого подвыражения. Для этого можно воснользоваться функцией applyop:

applyop(f, i, е) — применяет функцию f к i-му подвыражению выражения е applyop(f, i, е. ..., xk, ...) — применяет функцию f к i'-му подвыражении выражения е с передачей необязательных дополнительных аргументов xk.

Ниже даны примеры применения этой функции:

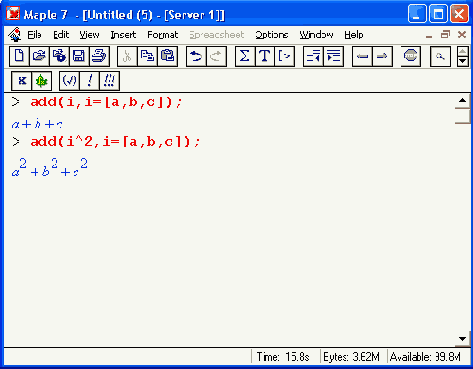
Подстановки с помощью функций add mul и seq

Подстановки с помощью функций add, mul и seq

Заметим, что операции, подобные описанным выше, Maple 7 реализует и с рядом других функций. Ограничимся примерами на подстановки с помощью функций сложения add, умножения mul и создания последовательностей seq:

Подстановки с помощью функций subs и subsop

Подстановки в общем случае служат для замены одной части выражения на другую. Частными видами подстановок являются такие виды операций, как замена одной переменной на другую или замена символьного значения переменной ее численным значением. Основные операции подстановки выполняют следующие функции: .,

subs(x=a.e) — в выражении е заменяет подвыражение х на подвыражение а; subs(sl,...,sn,e) — в выражении е заменяет одни подвыражения на другие, выбирая их из списков si, ..., sn вида х=а; subsop(eql, eq2, .... eqi, ...eqn, e) — в выражении е заменяет указанные в eqi операнды другими, указанными в правой части равенств eqi вида ni=ei, где ni — номер операнда, ei — выражение для замены.

Все эти функции возвращают измененное после подстановки выражение. Ниже показаны примеры применения функций подстановок:

Преобразование выражений

Еще одним мощным средством преобразования выражений является функция combine. Она обеспечивает объединение показателей степенных функций и преобразование тригонометрических и некоторых иных функций. Эта функция -может записываться в трех формах:

combine(f)

combinef(, n)

combine(f. n. optl. opt2. ...)

Здесь f — любое выражение, множество или список выражений; n — имя, список или множество имен; optl, opt2, ... — имена параметров. Во втором аргументе можно использовать следующие функции:

Преобразование выражений в тождественные формы

Многие математические выражения имеют различные тождественные формы. Порою преобразование выражения из одной формы в другую позволяет получить результат, более удобный для последующих вычислений. Кроме того, различные функции Maple 7 работают с разными формами выражений и разными типами данных. Поэтому большое значение имеет целенаправленное преобразование выражений и данных.

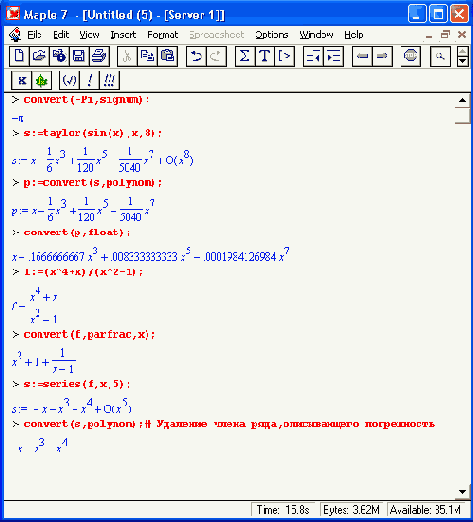
Основной функцией для такого преобразования является функция convert:

convert(expr. form, аrgЗ. ...)

Здесь ехрr — любое выражение, form — наименование формы, аrg3, ... — необязательные дополнительные аргументы.

convert — простая и вместе с тем очень мощная функция. Ее мощь заключается в возможности задания множества параметров. Их полный перечень (76 штук!) можно найти в справке по функции convert. Многие из этих параметров очевидны с первого взгляда, поскольку повторяют наименования типов чисел, данных или функций. Например, опции binary, decimal, hex и octal преобразуют заданные числа в их двоичное, десятичное, шестнадцатеричное и восьмеричное представление. Параметр vector задает преобразование списка в вектор (напоминаем, что список и вектор — разные типы данных), а параметр matrix — в матрицу. Приведем примеры применения функции convert:

Программирование символьных операций

Реализация итераций Ньютона в символьном виде

Найти достаточно простую и наглядную задачу, решение которой отсутствует в системе Maple 7, не очень просто. Поэтому для демонстрации решения задачи с применением аналитических методов воспользуемся примером, ставшим классическим, — реализуем итерационный метод Ньютона при решении нелинейного уравнения вида f(x) - 0.

Как известно, метод Ньютона сводится к итерационным вычислениям по следующей формуле:

xi+1=x1+f(x1)/f'(x1);

Реализующая его процедура выглядит довольно просто:

Работа с уровнями вложенности выражений

В общем случае выражения могут быть многоуровневыми и содержать объекты, расположенные на разных уровнях вложенности. Приведем две функции для оценки уровней выражений и списков:

nops(expr) — возвращает число объектов первого уровня (операндов) в выражении ехрr; ор(ехрr) — возвращает список объектов первого уровня в выражении ехрr; ор(n.ехрr) — возвращает n-й объект первого уровня в выражении ехрr.

Ниже представлены примеры применения этих функций:

Расширение выражений

Даже в жизни мы говорим: «не все так просто». Порою упрощенное выражение скрывает его особенности, знание которых является желательным. Функция expand «расширяет» выражение ехрr и записывается в виде:

expanc(expr, expr1, ехрг2, .... ехрrn)

где ехрr — расширяемое выражение, exprl, ехрг2, ..., ехрrn — необязательные подвыражения — опции. Имеется также инертная форма данной функции — Expand (ехрr). Кроме того, возможно применение операторной конструкции frontend(expans,[expr]).

Функция expand раскладывает рациональные выражения на простые дроби, полиномы на полиномиальные разложения, она способна раскрыть многие математические функции, такие как sin, cos, tan, sinh, cosh, tanh, det, erf, exp, factorial, GAMMA, In, max, min, Psi, binomial, sum, product, int, limit, bernoulli, euler, abs, signum, pochhammer, polylog, BesselJ, BesselY, Bessell, BesselK, AngerJ, Beta, Hankel, Kelvin, Struve, WeberE и функция piecewise. С помощью дополнительных аргументов expr1, ехрr2, ..., exprh можно задать расширение отдельных фрагментов в ехрr.

Примеры применения функции expand приведены ниже:

Разложение выражений (факторизация)

Для алгебраических выражений функция факторизации записывается в вычисляемой и не вычисляемой (инертной) формах:

factor(a) Factor(a)

factpr(a.K) Factor(а.К)

Здесь а — полином с несколькими переменными, К — необязательное алгебраическое расширение. Для получения результата от инертной формы функции факторизации надо использовать функции вычисления evala или evalgf.

Главная цель факторизации это нахождение максимального числа независимых сомножителей выражения, линейных по заданным переменным с коэффициентами наиболее простой формы. Ниже представлены примеры применения функции factor:

Обратите внимание на то, что

Шаг 1

Примечание 1
Примечание 1

Обратите внимание на то, что в предшествующих версиях Maple загрузка библиотеч ной функции cost выполнялась иначе — командой readlib(cost). Это обстоятельство может служить причиной неверной работы документов, созданных в старых версиях Maple, в среде описываемой версии Maple 7.

Вы можете проверить, что функция

Шаг 1

ПРИМЕЧАНИЕ
Вы можете проверить, что функция sort в Maple 7 способна сортировать буквы и даже слова русского языка.
Если функция сортировки меняет порядок расположения членов в выражении (или порядок расположения выражений), то другая функция — select — служит для выделения требуемого выражения:
select(f, e)
select(f, е. Ы. ..., bn)
Как бы обратной ей по действию служит функция remove, устраняющая заданные выражения:
remove(f, e)
remove(f, е, b1.... bn)
В этих функциях f — процедура, возвращающая логическое значение, е — список, множество, сумма, произведение или функция, b1, ..., bn — необязательные дополнительные аргументы.
Далее даны примеры применения этих функций.

Шаг 1

в аналитическом виде здесь используется

Шаг 1

Для получения итерационной формулы в аналитическом виде здесь используется функция unapply. Теперь, если задать решаемое уравнение, то можно получить искомое аналитическое выражение:

Прежние версии системы Maple не

Шаг 1

Прежние версии системы Maple не брали этот интеграл, поскольку он не имеет аналитического представления через обычные функции. Maple 7 блестяще вычисляет этот «крепкий орешек», но полученное выражение довольно сложно.
Из математики известно, что такой интеграл может быть представлен в следующем виде:

Вначале подготовим процедуру IntExpMonomialR, реализующую

Шаг 1

где р(х) — выражение, представляющее полином.
Приведенный ниже пример подготовлен в реализации Maple 7 [38]. Вначале подготовим процедуру IntExpMonomialR, реализующую вычисление уже рассмотренного ранее интеграла, но рекурсивным способом:

и более сложные примеры на

Шаг 1

Рекомендуется просмотреть и более сложные примеры на применение этих функций в справке.

Шаг 1

Эти примеры далеко не исчерпывают

Шаг 1

Эти примеры далеко не исчерпывают возможностей функции combine в преобразовании выражений. Рекомендуется обзорно просмотреть примеры применения функции combine с разными параметрами, приведенные в справочной системе Maple 7.

Шаг 1

Из этих примеров нетрудно заметить,

Шаг 1

Из этих примеров нетрудно заметить, что если второй параметр функции mар — список, то функция (первый параметр) прикладывается к каждому элементу списка, так что возвращается также список. Из последнего примера видно, что если за вторым параметром идет перечисление аргументов, то они включаются в список параметров функции.
Функция mар2 отличается иным расположением параметров. Ее действие наглядно поясняют следующие примеры:

Шаг 1

Maple имеет также оператор селекции

Шаг 2

Maple имеет также оператор селекции А[ехрr]. Его действие поясняют следующие примеры:

Действие функции simplify существенно зависит

Шаг 2

Действие функции simplify существенно зависит от областей определения переменных. В следующем примере упрощение выражения не произошло, поскольку результат этой операции неоднозначен:

Шаг 2

можно получить результаты вычислений для

Шаг 2

Далее, задав начальное приближение для х в виде х = х0, можно получить результаты вычислений для ряда итераций:

Используя эту формулу, мы можем

Шаг 2

Используя эту формулу, мы можем создать простую процедуру для численного и аналитического вычисления данного интеграла:

Теперь составим процедуру для вычисления

Шаг 2

Теперь составим процедуру для вычисления по частям нашего интеграла:

их список читатель может пополнить

Шаг 2

Из этих примеров ( их список читатель может пополнить самостоятельно) следует, что функция преобразования convert является одной из самых мощных функций Maple. С ее помощью можно получить множество различных форм одного и того же выражения.

Шаг 2

Следует обратить внимание на то,

Шаг 2

Следует обратить внимание на то, что результат подстановок, полученный с помощью функции subop, порой может не совпадать с ожидаемым. Поэтому полезно контролировать получаемые в результате подстановок выражения на их корректность.
Одним из важных применений подстановок является проверка правильности решений уравнений и систем уравнений. Ниже дан пример такой проверки:

Шаг 3

определив переменные как реальные или

Шаг 3

Однако, определив переменные как реальные или положительные, можно легко добиться желаемого упрощения:

Нетрудно заметить, что, испытав скачок

Шаг 3

Нетрудно заметить, что, испытав скачок в начале решения, значениях довольно быстро сходятся к конечному результату, дающему корень заданной функции. Последние три итерации дают одно и то же значение х. Заметим, что этот метод дает только одно решение, даже если корней несколько. Вычислить другие корни в таком случае можно, изменив начальное условие.
Можно попробовать с помощью полученной процедуры получить решение и для другой функции:

в аналитическом виде довольно прост

Шаг 3

Результат в аналитическом виде довольно прост для данного интеграла с конкретным значением т. Более того, мы получили несколько иной результат и дляп в общем случае. Но точен ли он? Для ответа на этот вопрос продифференцируем полученное выражение:

В этой процедуре имеется обращение

Шаг 3

В этой процедуре имеется обращение к ранее составленной процедуре IntExpMonomialR. Обратите внимание на то, что в процедуре введено предупреждение об определенных проблемах, связанных с использованием функции degree (сообщение начинается с символов ###). Тем не менее процедура работает, в чем убеждают по крайней мере следующие примеры:

Здесь задана система из трех

Шаг 3

Здесь задана система из трех нелинейных уравнений, которая затем решена функцией solve. В конце примера с помощью функции подстановки выполнена проверка правильности решения. Оно верно, поскольку у всех уравнений значение левой части совпадает со значением правой части.

Шаг 4

Читателю настоятельно рекомендуется просмотреть все

Шаг 4

Читателю настоятельно рекомендуется просмотреть все разделы справочной системы, относящиеся к примерам применения функции simplify (в том числе с другими функциями символьных преобразований), поскольку их число очень велико и эти примеры наглядно демонстрируют необходимость правильного применения разнообразных параметров для придания упрощениям нужного характера. Если функция simplify не способна выполнить упрощение выражения ехрr, то она просто его повторяет. Это сигнал к применению опций.

и вполне естественно) уже другой

Шаг 4

Здесь итерационная формула имеет ( и вполне естественно) уже другой вид, но сходимость к корню также обеспечивается за несколько итераций. ;
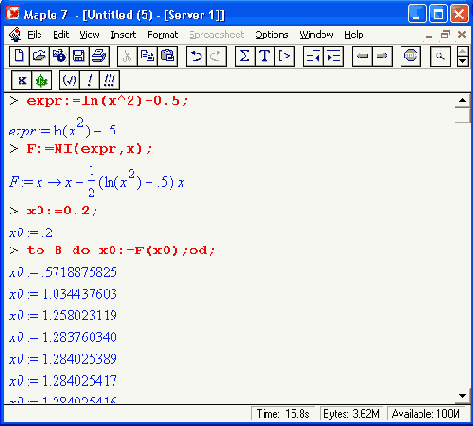
Возможна и иная форма задания итерационной процедуры с применением оператора дифференцирования D и заданием исходной функции также в виде процедуры:

Результат дифференцирования выглядит куда сложнее,

Шаг 4

Результат дифференцирования выглядит куда сложнее, чем вычисленный интеграл. Однако с помощью функции simplify он упрощается к подынтегральной функции:

В заключение остается отметить, что

Шаг 4

В заключение остается отметить, что данный пример в Maple V R4 дает неточный результат, хотя никаких сообщений об ошибках не выводится.

в программных процедурах можно использовать

Шаг 5

Вообще говоря, в программных процедурах можно использовать любые операторы и функции, присущие Maple-языку, в том числе и те, которые реализуют символьные вычисления. Это открывает широкий простор для разработки новых процедур и функций, обеспечивающих выполнение символьных операций.

о том, что задача вычисления

Шаг 5

Это говорит о том, что задача вычисления заданного интеграла в аналитической форме действительно решена. А что касается громоздкости результатов, так ведь системы, подобные Maple 7, для того и созданы, чтобы облегчить нам работу с громоздкими вычислениями — в том числе аналитическими.

Упрощение выражений

Функция simplify — одна из самых мощных в системах символьной математики. Она предназначена для упрощения математических выражений. «Все гениальное просто», — любим мы повторять, хотя это далеко не всегда так. Тем не менее стремление представить многие математические выражения в наиболее простом виде поощряется в большинстве вычислений и нередко составляет их цель. В системе Maple 7 функция упрощения используется в следующем виде:

simplify(expr) — возвращает упрощенное выражение ехрr или повторяет его, если упрощение в рамках правил Maple 7 невозможно; simplify(expr, nl, n2, ...) —возвращает упрощенное выражение ехрr с учетом параметров с именами nl, n2, ... (в том числе заданных списком или множеством); simplify(ехрг,assume=prop) — возвращает упрощенное выражение ехpr с учетом всех условий.

Функция simplify — многоцелевая. Она обеспечивает упрощение математических выражений, выполняя следующие типовые действия (для простоты обозначим их как ->):

комбинируя цифровые подвыражения (3*х*5->15*х, 10*х/5->2*х); приводя подобные множители в произведениях (х^3*а*х->а*х^4); приводя подобные члены в суммах (5*х+2+3*х->8*х+2); используя тождества, содержащие ноль (а+0->а, х-0->х); используя тождества, содержащие единицу (1*х->х); распределяя целочисленные показатели степени в произведениях ((3*x*y^3)^2 ->9*х^2*у^6); сокращая ехрr на наибольший общий полиномиальный или иной множитель; понижая степень полиномов там, где это возможно; используя преобразования, способные упростить выражения.

Несмотря на свою гибкость, функция simplify не всегда способна выполнить возможные упрощения. В этом случае ей надо подсказать, в какой области ищутся упрощения и где можно найти соответствующие упрощающие преобразования.

С этой целью в функцию simplify можно включать дополнительные параметры.

В качестве параметров могут задаваться имена специальных математических функций и указания на область действия упрощений: Bessell, BesselJ, BesselK, BesselY, Ei, GAMMA, RootOf, LambertW, dilog, exp, In, sqrt, polylog, pg, pochhammer, trig (для всех тригонометрических функций), hypergeom, radical, power и atsign (для операторов). Полезен также параметр symbolic, явно указывающий на проведение символьных преобразований.

Возможно также применение функции simplify в форме simplify[<name>], где <name> — одно из следующих указаний: atsign, GAMMA, hypergeom, power, radical, RootOf, , sqrt, trig. Ниже даны примеры применения функции Simplifу:

Вложенные процедуры и интегрирование по частям

Теперь мы подошли к важному моменту, о котором читатель наверняка уже давно догадался — в составляемых пользователем процедурах можно использовать ранее составленные им (или кем-то еще) другие процедуры! Таким образом, Maple-язык позволяет реализовать процедуры, вложенные друг в друга. Для иллюстрации применения вложенных процедур рассмотрим операцию интегрирования по частям. Пусть нам надо вычислить интеграл:

Вычисление интеграла по известной формуле

Рассмотрим следующий пример: