Функции интегрирования пакета student
В пакетах Maple 7 можно найти множество специальных функций для вычисления интегралов различного типа. Например, в пакете student имеются следующие функции:
Int(expr,x) — инертная форма вычисления неопределенного интеграла; Doubleint(expr,x,y,Domain) — вычисление двойного интеграла по переменным х и у по области Domain; Tripleint(expr,x,y,z) — вычисление тройного интеграла; intparts(f,u) — интегрирование по частям.Ниже дан пример применения функции Tripleint пакета student:
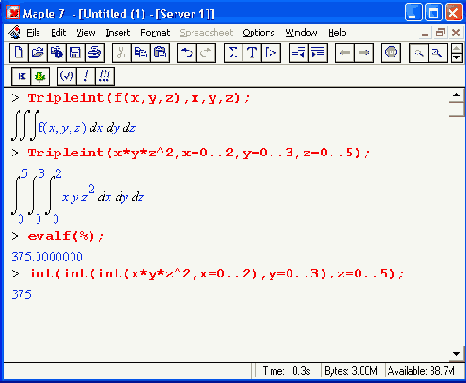
Объективности ради надо отметить, что вычисление тройного интеграла с помощью функции Tripleint занимает много времени (около 20 с на компьютере с процессором Pentium II 350 МГц). 'Однако тот же результат (см. последний пример) получается за доли секунды при использовании тройного интегрирования с помощью функции int.
Функции maximize и minimize
Главными из этих функций являются maximize и minimize, оптимизирующие задачу симплекс-методом. Они записываются в следующих формах:
maximize(f, С)
minimize(f, С)
maximize(f , С, vartype)
nrinimize(f , С, vartype)
maximize(f , С,vartype, 'NewC', 'transform')
m'inimize(f , C, vartype, 'NewC', 'transform')
Здесь f — линейное выражение, С — множество или список условий, vartype — необязательно задаваемый тип переменных NONNEGATIVE или UNRESTRICTED, NewC и transform — имена переменных, которым присваиваются соответственно оптимальное описание и переменные преобразования. Ниже даны^примеры применения этих функций:
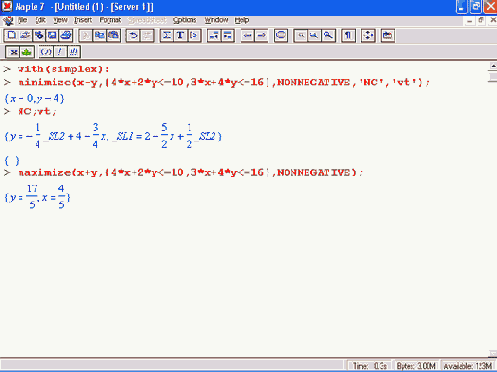
Функции пакета student
Пакет student — это, несомненно, один из пакетов, наиболее привлекательных для студентов и аспирантов. В нем собраны наиболее распространенные и нужные функции, которые студенты университетов и иных вузов обычно используют на практических занятиях, при подготовке курсовых и дипломных проектов. Набор этих функций, разумеется, не ограничивается «скромными» потребностями студентов — просто это наиболее распространенные функции, в основном относящиеся к математическому анализу. Наряду со студентами эти функции широко используют профессионалы-математики и ученые, применяющие математические методы в своей работе.
В этом пакете имеется почти полсотни функций:
D — дифференциальный оператор; Diff — инертная форма функции вычисления производной; Doubleint — инертная форма функции вычисления двойного интеграла; Int — инертная форма функции интегрирования int; Limit — инертная форма функции вычисления предела limit; Lineint — инертная форма функции вычисления линейного интеграла lineint; Point — тестирование объекта на соответствие типу точки (point); Product — инертная форма функции вычисления произведения членов последовательности; Sum — инертная форма функции вычисления суммы членов последовательности; Tripleint — инертная форма функции вычисления тройного интеграла; changevar — замена переменной; combine — объединение подобных членов; completesquare — вычисление полного квадрата (многочлена); distance — вычисление расстояния между точками; equate — создание системы уравнений из списков, таблицы, массивов; extreme — вычисление экстремума выражения; integrand — вывод подынтегрального выражения из-под знака инертного интеграла; intercept — нахождение точки пересечения двух кривых; intparts — интегрирование по частям; isolate — выделение подвыражения; leftbox — графическая иллюстрация интегрирования методом левых прямоугольников; leftsum — числовое приближение к интегралу левыми прямоугольниками; makeproc — преобразование выражения в процедуру Maple; maximize — вычисление максимума функции; middlebox — графическая иллюстрация интегрирования методом центральных прямоугольников; middlesum — числовое приближение к интегралу центральными прямоугольниками; midpoint — вычисление средней точки сегмента линии; minimize — вычисление минимума функции; powsubs — подстановка для множителей выражения; rightbox — графическая иллюстрация интегрирования методом правых прямоугольников; rightsum — числовое приближение к интегралу правыми прямоугольниками; showtangent — график функции и касательной линии; simpson — числовое приближение к интегралу по методу Симпсона; slope — вычисление и построение касательной к заданной точке функции; trapezoid — числовое приближение к интегралу методом трапеций; value — вычисление инертные функции.Генерация случайных чисел с заданным распределением
Основой этого подпакета является функция random:
random[distribution] (quantity,unifarm,method)
или
stats[random, distribution] (quantity,unifofm,method)
где
distribution — описание закона распределения случайных чисел; quantity — положительное число, указывающее на количество получаемых случайных чисел (по умолчанию 1, возможен параметр 'generator'); uniform — процедура генерации чисел с равномерным распределением или ключевое слово 'default' (по умолчанию); method — указание на один из трех методов ('auto', 'inverse' или 'builtin').Возможно задание дискретных и непрерьвных распределений, например binomiald --дискретное биномиальное распределение, discreteumform — дискретное 'равномерное распределение, empirical — дискретное эмпирическое распределение, poisson — дискретное распределение Пуассона, beta — бета-распределение, cauchi — .распределение Коши, exponential — экспоненциальное и др. (есть функции практически для всех известных распределений).
Следующие примеры демонстрируют технику получения случайных чисел с заданным законом распределения;
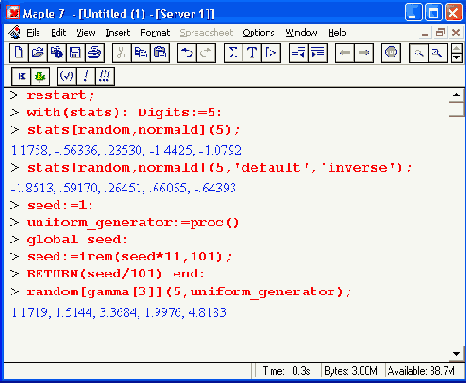
Графика статистического пакета stats
Статистический пакет stats имеет свою небольшую библиотечку для построения графиков. Она вызывается в следующем виде:
stats[statplots, function](args)
или
statplots[function](args)
Вид графика задается описанием function: boxplot, histogram, notehedbox, quantile, quantile2, scatterld, scatter2d и symmetry. Данные функции обеспечивают построение типовых графиков, иллюстрирующих статистические расчеты. В качестве примера на рис. 16.13 показано задание множества случайных точек и его отображение на плоскости в ограниченном прямоугольником пространстве.
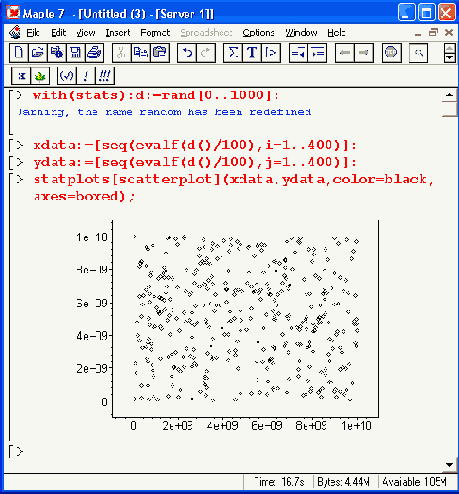
Рис. 16.13. Создание случайных точек и построение их на плоскости
По равномерности распределения точек можно судить о качестве программного генератора случайных чисел, встроенного в Maple 7.
Довольно часто для визуализации вычислений используется построение гистограмм. Для их создания пакет stats имеет функцию histogram:
stats[statplotsб histogram](data) :
statplots[h1stogram](data)
stats[statplots, histogram[scale](data)
statp1ots[histogram[scale](data)
Здесь data — список данных, scale — число или описатель. Детали применения этой простой функции поясняет рис. 16.14. На нем дан два примера — построение столбцов заданной ширины и высоты и построение гистограммы 100 случайных чисел с нормальным распределением.
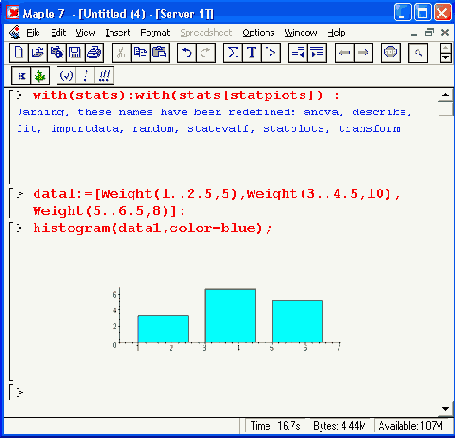
Рис. 16.14. Построение гистограмм
Обратите внимание на то, что для второго примера гистограмма будет несколько меняться от пуска к пуску, так как данные для ее построения генерируются случайным образом.
Характеристика пакета stats
Мир математических систем сейчас насыщен статистическими системами, например такими, как Statistica или StatGraphics. Они прекрасно приспособлены для решения задач статистической обработки обширных массивов данных. Тем не менее проведение статистических расчетов в Maple 7 возможно и в ряде случаев весьма целесообразно — например, когда они являются частью исследовательского проекта.
Пакет stats для таких расчетов представлен всего двумя многоцелевыми статистическими функциями:
stats[subpackage, functionj(args)
subpackage[function](args)
Однако благодаря специальной форме задания параметров (в частности, в виде подпакетов — subpackages) возможно вычисление самых разнообразных статистических функций. Имеются следующие подпакеты:
anova — вариационный анализ; describe — функции распределения вероятности; fit — регрессионный анализ; random — генерация случайных чисел с различными законами распределения; statevalf — вычисление статистических функций и получение оценок для массивов данных; statplots — построение графиков статистических функций; transform — функции преобразования данных.Иллюстративная графика пакета student
Пакет student имеет три графические функции для иллюстрации интегрирования методом прямоугольников:
leftbox(f(x), x=a..b, о) или leftbox(f(x), x=a..b, n, 'shading'=<color>, о); rightbox(f(x), x=a..b, о) или rightbox(f(x), x=a..b, n, о); middlebox(f(x), x=a..b, о) или middlebox(f(x), x=a..b, n, o);Здесь f (x) — функция переменной х, х — переменная интегрирования, а — левая граница области интегрирования, b — правая граница области интегрирования, n — число показанных прямоугольников, color — цвет прямоугольников, о — параметры (см. ?plot,options).
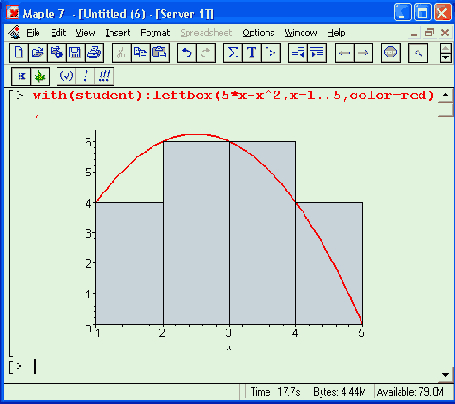
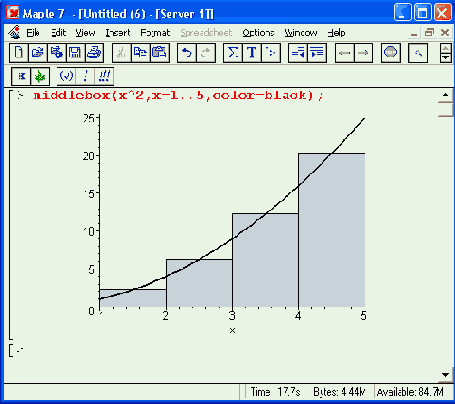
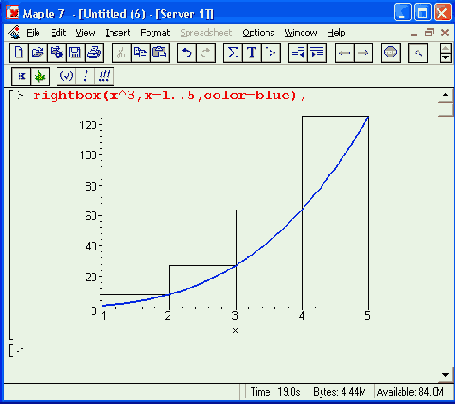
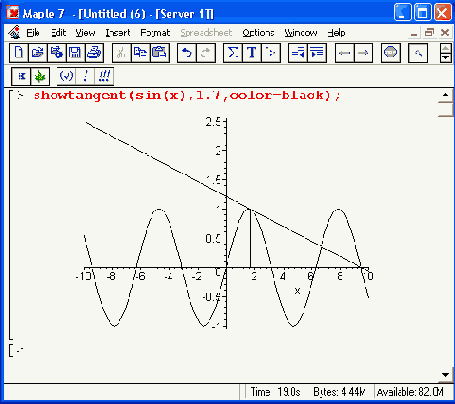
Рис. 16.16. Примеры иллюстративной графики пакета student
В этих функциях прямоугольники строятся соответственно слева, справа и по середине относительно узловых точек функции f(x), график которой также строится. Кроме того, имеется функция для построения касательной к заданной точке х = а для линии, представляющей f(x):
showtangent (f(x), x = а)
Рисунок 16.16 показывает все эти возможности пакета student. Три вида графиков здесь построены в отдельных окнах.
Графические средства пакета student ограничены. Но они предоставляют как раз те возможности, которые отсутствуют в основных средствах построения графиков.
Инструментальный пакет для линейных рекуррентных уравнений LREtools
Этот пакет полезен математикам, часто использующим рекуррентные отношения и формулы. Он дополняет функцию rsolve основной библиотеки и содержит следующие функции: :
> with(LREtools):
[REcontent, REcreate, REplot, REprimpart, REreduceorder, REtoDE,REtodelta, REtoproc, autodispersion, constcoeffsol,
5,dispersion, divconq, firstlin, hypergeomsols, polysols,ratpolysols, riccati, shift]
С назначением функций этого пакета можно познакомиться по справочной системе Maple 7.
Набор функций пакета geom3d
Помимо существенного расширения пакета geometry в систему Maple 7 введен новый геометрический пакет geonfld. Он предназначен для решения задач в области трехмерной геометрии. При загрузке пакета появляется доступ к большому (свыше 140) числу новых функций:
> with(geom3d);
[Archimedean, AreCollinear, AreConcurrent, AreConjugate, AreCoplanar, AreDistinct, AreParallel, ArePerpendicular, AreSameObjects, AreSamePlane, AreSkewLines, DefinedAs, DirectionRatios, Equation,'FindAngle, FixedPoint, GlideReflect, GlideReflection, GreatDodeeahedron, Greatlcosahedron, GreatRhombicuboctahedron, GreatRhombiicosidodecahedron,
GreatStellatedDodecahedron,HarmonicConjugate,
HexakisIcosahedron,Hexakis Octahedron, JnRadius,
Is Archimedean, IsEquilateral, IsFacetted,
IsOnObject, IsQuasi,hRegular,
IsRightTriangletIsStellated,IsTangent,
MidRadius, NormalVector, OnSegment, ParallelVector, PentagonalHexacontahedron, PentagonallcositetrahedronjPentakisDodecahedron, QuasiRegularPolyhedron,
RadicalCenter, RadicalLine,RadicalPlane, RegularPolyhedron, RhombicDodecahedron, RhombicTriacontahedron, Rotatory Reflect, Rotatory Reflection, ScrewDisplace, ScrewDisplacement, SmallRhombicubactahedron, SmallRhombiicosidodecahedron, SmallStellatedDodecahedron, SnubCube, SnubDodecahedron, StereographicProjection, StretchRotate, TangentPlane,
TetrakisHexahedron, TrapezoidalHexecontahedron, Trapezoidallcositetrahedron, Triakislcosahedron, TriakisOctahedron, TriakisTetrahedron, TruncatedCuboctahedron, TruncatedDodecahedron,TruncatedHexahedron, Truncatedlcosahedron, Truncatedlcosidodecahedron, TruncatedOctahedron, TruncatedTetrahedron, altitude, area, center, centroid, circle, coordinates, cube,
cuboctahedron, detail, dilate, distance, dodecahedron, draw, dsegment, duality,faces, facet, form, gtetrahedron, hexahedron, homology, homothety, icosahedron, icosidodecahedron, identity, incident, intersection, inverse, inversion, line, midpoint, octahedron, parallel, parallelpiped, plane, point, polar, pole, powerps, projection, radius, rqndpoint, reflect^ reflection, rotate, rotation, schlafli, segment, sides, sphere, stellate, tetrahedron, tname, transform, translate, translation, transprod, triangle, unit, valuesubs, vertices, volume, xcoord, xname, ycoord, yname, zcoord, zname ]
Функции этого пакета обеспечивают задание и определение характеристик и параметров многих геометрических объектов: точек в пространстве, сегментов, отрезков линий и дуг, линий, плоскостей, треугольников, сфер, регулярных и квазирегулярных полиэдров, полиэдров общего типа и др. Для описания функций этого пакета пришлось бы воспроизвести обширное справочное руководство по стереометрии. В то же время назначение функций ясно из их названия, а характер применения тот же, что для функций описанного выше пакета geometry.
Набор функций пакета geometry
Пакет геометрических расчетов geometry в системе Maple 7 получил как бы второе рождение число его функций по сравнению с версией этого пакета в системе Maple V R5 возросло в несколько раз. Теперь загрузка пакета возвращает весьма внушительный список из более чем 100 функций:
> with(geometry);
[Appolonius, AreCollinear, AreConcurrent, AreConcyclic, AreConjugate, AreHarmonic, AreOrthogonal, AreParallel, ArePerpendicular, AreSimilar, AreTangent, CirdeQfSimilitude,CrossProduct, CrossRatio, DefinedAs, Equation, EulerCircle, EulerLine, Exterior Angle, ExternalBisector, FindAngle, GergonnePoint, GlideRefledion, HorizontalCoord, HorizontalName, InteriorAngle, IsEquilateral,
IsOnCircle, IsOnLine, IsRightTriangle, MajorAxis, MakeSquare, MinorAxis,NagelPoint, OnSegment, ParallelLine, PedalTriangle, PerpenBisector, PerpendicularLine, Polar, Pole, RadicalAxis, RadicalCenter, RegularPolygon, RegularStarPolygon, SensedMagnitude, SimsonLine, SpiralRotation, StretchReflection, StretchRotation, TangentLine, VerticalCoord, VerticalName,
altitude, apothem, area, asymptotes, bisector, center, centroid, circle, circumcircle, conic, convexhull, coordinates, detail, diagonal, diameter, dilatation, directrix, distance, draw, dsegment, ellipse, excircle, expansion, foci, focus, form, homology, homothety, hyperbola, incircle, inradius, intersection, inversion, line, medial, median, method, midpoint, orthocenter, parabola, perimeter, point, powerpc, projection,
radius, randpoint, reciprocation, reflection, rotation, segment, sides, similitude, slope, square, stretch, tangentpc, translation, triangle, vertex, vertices}
Этот пакет содержит средства расчета основных параметров ряда геометрических объектов. Для каждого объекта возможно задание различных исходных величин, так что пакет охватывает практически все виды классических геометрических расчетов на плоскости. Несомненно, этот пакет заинтересует всех, кто работает в области геометрии и смежных областях.
Обратите внимание на то, что многие функции этого пакета вовсе не рисуют на экране соответствующие фигуры, а лишь выполняют типовые геометрические расчеты. Разумеется, в дальнейшем, используя результаты этих расчетов, можно построить соответствующую фигуру с помощью графических функций.
Набор функций пакета networks
Графы широко используются при решении многих прикладных и фундаментальных задач. Пользователей, занятых решением таких задач, наверняка порадует пакет networks, содержащий весьма представительный набор функций:
> with(networks);
Warning, the names diameter, draw and vertices have been redefined[acycpoly, addedge, addvertex, adjacency, allpairs, ancestor, arrivals,bicomponents, charpoly, chrompoly, complement, complete, components, connect, connectivity, contract, countcuts, counttrees, cube,cycle, cyclebase, daughter, degreeseq, delete, departures, diameter,dinic, djspantree, dodecahedron, draw, duplicate, edges, ends,eweight,flow,flowpoly,fundcyc, getlabel, girth, graph, graphical,gsimp,gunion,
head, icosahedron, incidence, incident, indegree, induce, isplanar,maxdegree, mincut, mindegree, neighbors, new, octahedron, outdegree,path,petersen, random, rank, rankpoly, shortpathtree, show,shrink, span, spanpoly, spantree, tail, tetrahedron, tuttepoly, vdegree,vertices, void, vweight]
Объективности ради надо отметить, что в Maple 7 из этого пакета удалено несколько второстепенных функций, которые были в версии Maple V R5. Теория графов используется достаточно широко даже при решении прикладных задач — например, для вычисления оптимальных маршрутов движения железнодорожных составов, наиболее целесообразной раскройки тканей и листов из различных материалов и т. д.
Новая функция Maple 7 plot_real_curve
В пакет расширения algcurves добавлена новая функция импликативной графики plot_real_curve. Она строит алгебраическую кривую для действительной части полиномиального выражения и записывается в виде:
plot_real_curve (p, х, у, opt)
Функция имеет следующие параметры:
р — полиномиальное выражение переменных х и у задающее алгебраическую кривую; opt — параметр, который может быть записан в форме приведенных ниже выражений: showArrows = true или false — задает показ стрелок касательных или перпендикулярных к точкам вдоль кривой (по умолчанию false); arrowIntervalStep = posint — задает число точек, пропускаемых до показа очередной пары стрелок (по умолчанию 10); arrowScaleFactor = positive — задает масштаб для длины стрелок (по умолчанию 1); colorOfTangentVector = с — задает цвет касательных стрелок, по умолчанию заданный как зеленный, COLORCRGB,0,1,0); colorOfNormalVector = с — задает цвет перпендикулярных стрелок, по умолчанию заданный как красный, COLOR (RGB ,1,0,0); colorOf Curve = с — задает цвет кривой, по умолчанию заданный как синий, COLOR(RGB, 0, 0, 1); eventTolerance = positive — задает погрешность при представлении сингулярных точек (по умолчанию 0,01); NewtonTolerance = positive — задает погрешность при выполнении ньютоновских итераций в ходе построений.Функция plot_real_curve вычисляет и строит алгебраическую кривую по точкам и может (при использовании параметра opt) строить стрелки-векторы по касательным и перпендикулярным направлениям к каждой точке или к части точек. Возможно задание разных цветов для кривой и стрелок. Применение функции plot_real_curve показывает рис. 16.8.
При задании построения стрелок касательные стрелки строятся по внешней части кривой и указывают направление ее построения. Перпендикулярные стрелки строятся по внутренней части кривой. Нетрудно заметить, что острие стрелки указывается только для длинных стрелок. Короткие стрелки острия не имеют и отображаются как отрезки прямых линий. Построение стрелок оказывается не вполне точным, если разнятся масштабы графика по горизонтали и вертикали, что можно подметить при внимательном рассмотрении графика на рис. 16.8, сверху.
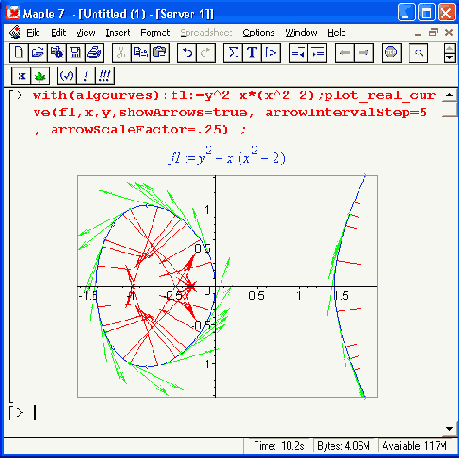
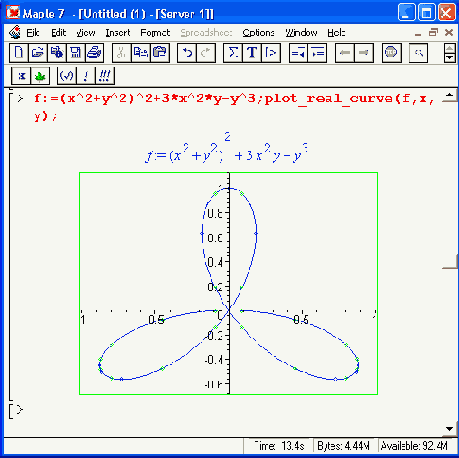
Рис. 16.8. Примеры применения функции plot_real_curve
Обзор пакетов узкого назначения
Мы уже не раз обращали внимание читателя на выборочный характер описания системы Maple 7 в данной книге. Хотя она и является одной из самых полных книг по данной системе, книга не претендует на роль детального справочника по Maple 7: Более того, такого справочника в виде книги нет и, вероятно, учитывая быстрые темпы модернизации программы, так и не будет. Для подобного описания Maple пришлось бы подготовить многотомное издание, охватывающее практически все области математики.
Учитывая это, мы вынуждены отказаться от попытки описать ряд пакетов специального назначения. Такими пакетами интересуются серьезные специалисты в области математики и им (не без труда, разумеется) под силу разобраться с назначением функций таких пакетов и примерами их применения, приведенными в справочной системе Maple 7. В связи с выше сказаннным, мы ограничимся перечислением оставшихся неизученными пакетов.
Обзор средств пакета
Задачи линейной оптимизации важны как в фундаментальных, так и в прикладных приложениях математики. В пакете simplex имеется небольшой, но достаточно представительный набор функций и определений для решения таких задач:
> with(simplex);
Warning, the protected names maximize and minimize have been redefined and unprotected
[basis, convexhull, cterm, deftne_zero, display, dual,feasible, maximize, minimize,pivot, pivoteqn, pivotvar, ratio, setup, standardize ]
Приведем краткое назначение этих функций:
basis — возврат списка основных переменных для множества линейных уравнений; convexhull — вычисление выпуклой оболочки для набора точек; cterm — задание констант для системы уравнений или неравенств; define_zero — определение наименьшего значения, принимаемого за ноль (по умолчанию увязано со значением системной переменной Digits); display — вывод системы уравнений или неравенств в матричной форме; dual — выдача сопряженных выражений; , equality — параметр для функции convert, указывающий на эквивалентность; feasible — выяснение возможности решения заданной задачи: maximize — вычисление максимума функции; minimize — вычисление минимума функции; pivot — создание новой системы уравнений с заданным главным элементом; pivoteqn — выдача подсистемы уравнений для заданного главного элемента; pivotvar — выдача переменных с положительными коэффициентами в целевой функции; ratio — выдача отношений для определения наиболее жесткого ограничения; setup — задание системы линейных уравнений; standardize — приведение заданной системы уравнений или неравенств к стандартной форме неравенств типа «меньше или равно». |
 |
Пакет алгебры линейных операторов Ore_algebra
Пакет Ore_algebra содержит набор функций алгебры линейных операторов, состав которого виден после обращения к пакету:
> with(0re_algebra);
[OrejoJDESol, Ore_to_RESol, Orejojdiff, Ore_to_shift, annihilators, applyopr, diff_algebra, poly, algebra, qshiji_algebra, rand_skew_poly, shift_algebra, skew_algebra, skewjslim, skewjgcdex, skewjydiv, skewjxrwer, skew_prem, skew_product]
Этот пакет поддерживает решение задач в области алгебры линейных операторов.
Пакет для работы с алгебраическими кривыми algcurves
Пакет для работы с алгебраическими кривыми прекрасно дополняет возможности геометрических пакетов. При обращении к нему он дает доступ к полутора десяткам функций:
> restart;with(algcurves);
[Weierstrassform, differentials, genus, homogeneous, homology, integral_basis, isjiyperelliptic, j_invariant, monodromy,parametrization ,periodmatrix,plot_knot,puiseux, singularities ]
Ввиду важности функций пакета и их сравнительно небольшого числа приведем полную форму записи функций и их назначение:
Weierstrassform(f ,x,y,x0,y0.opt) — вычисление нормальной формы для эллиптических или гиперболических алгебраических кривых; differentials(f, x, у, opt) — вычисление голоморфных дифференциалов алгебраических кривых; genus(f ,x,y,opt) — проверка подлинности алгебраической кривой; homogeneous (f, x, у, z) — создание полинома двух переменных, гомогенного в трех переменных; homo!ogy(f, x, у) — нахождение канонического гомологического базиса по алгоритму Треткоффа; integral_basis(f, x, у, S) — нахождение интегрального базиса алгебраического поля функции; is_hyperelliptic(f. х, у) — тестирование кривой на ее принадлежность к гиперболической; j_invariant(f ,x,y) — вычисление инварианта алгебраической кривой; monodromy(f, х, у, opt) — вычисляет монодромию алгебраической кривой; parametrization(f .x,y,.t) — нахождение параметризации для кривой с родом (даваемым функцией genuc), равным 0; periodmatrix(f, х, у, opt) — вычисление периодической матрицы кривой; plot_knot(f ,.x,.y,.opt) — построение узла — несамопересекающейся замкнутой кривой в трехмерном евклидовом пространстве; puiseux(f ,х=р,у,.n,.Т) — определение Пуизе- расширения алгебраической функции (может иметь и более простые формы записи); singularities(f ,x,y) — анализ кривой на сингулярность.Пакет для работы с гауссовыми целыми числами Gausslnt
Гауссово целое число — это число вида а + I*b, где а и b — любые целые рациональные числа. Таким образом, они образуют решетку всех точек с целыми координатами на плоскости комплексных чисел. Пакет Gausslnt содержит достаточно представительный набор функций для работы с этими числами:
> with(GaussInt):
Warning, the name GIgcd has been redefined
[GIbasis, Glchrem, GIdivisor, GIfacpoly, GIfacset, GIfactor, GIfactors, GIgcd, GIgcdex, Glhermite, Glissqr, Gllcm, GImcmbine, GInearest, GInodiv, GInorm, Glnormal, Glorder, GIphi, GIprime, Glquadres, Glquo, GIrem, GIroots, GIsieve, GIsmith ,GIsqrfree, GIsqrt, Glunitnormal ]
Нетрудно заметить, что в этот набор входят уже известные числовые функции, к именам которых добавлены буквы 61. Например, функция GIfactor(c) раскладывает гауссово число (в том числе комплексное) на простые множители, GIgcd(cl, с2) находит наибольший общий делитель гауссовых чисел cl и с2 и т. д. Функции этого пакета достаточно просты, так что ограничимся приведенными примерами. Гауссовы целые числа в большинстве научно-технических расчетов встречаются крайне редко. Так что этот пакет рассчитан на специалистов-математиков, работающих в области теории чисел.
Пакет для работы с р-адическими числами padic
Этот весьма специфический пакет содержит следующие функции для работы с р-адическими числами:
> with(padic);
[arccoshp, arccosp,arccothp, arccotp, arccschp, arccscp, arcsechp, arcsecp, arcsinhp, arcsinp, arctanhp, arctanp, coshp, cosp, cothp, cotp, cschp, cscp, evalp, expansion, expp, Icoeffp, logp, orderp, ordp, ratvaluep, rootp, sechp, seep, sinhp,sinp, sqrtp, tanhp,tanp, valuep]
В Maple 7 число функций этого пакета увеличено почти в четыре раза. Однако ввиду специфичности данных функций их изучение мы оставляем за читателем для самостоятельной работы.
Пакет для работы с рациональными производящими функциями genfunc
В пакете genfunc, предназначенном для работы с производящими функциями, содержатся следующие средства:
> with(genfunc);
[rgf_charseq, rgf_encode, rgf_expqnd, rgfjindrecur, rgfjiybrid, rgfjiorm, rgf_pfrac, rgf_relate, rgf_sequence, rgf_simp, rgfjerm,termscale]
Эти функции представляют специальный интерес для пользователей, работающих в области теории чисел и рациональных функций.
Пакет для работы с рядами ортогональных многочленов OrthogonalSeries
Новый пакет для работы с рядами ортогональных многочленов OrthogonalSeries имеет довольно представительный набор функций:
> with(OrthogonalSeries);
[Add, Apply Operator, ChangeBasis, Coefficients, ConvertToSum, Copy, Create, Degree, Derivate, DerivativeRepresentation, Evaluate, Getlnfo, Multiply, PolynomialMultiply, ScalarMultiply, SimplifyCoefficients, Truncate]
Поскольку этот пакет представляет интерес в основном для опытных математиков, мы не будем рассматривать его функции (в целом достаточно простые) подробно и ограничимся несколькими примерами. В следующем примере с помощью функции Create создается бесконечный ряд с ортогональным многочленом Эрмита в составе базового выражения ряда:

В другом примере показано представление полиномиального выражения в новом базисе с ортогональными многочленами Чебышева с помощью функции ChangeBasis:
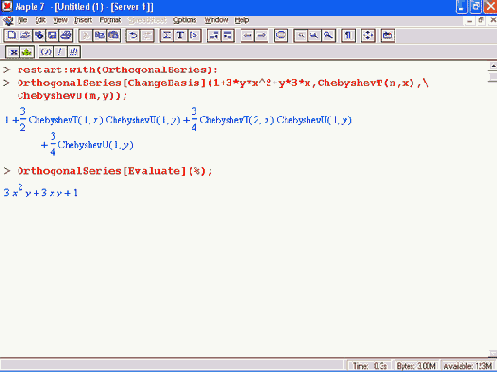
Обратите внимание на то, что новое выражение после исполнения команды Evaluate приняло вид исходного выражения.
Следующий пример демонстрирует создание ряда на основе ортогональных многочленов Чебышева и его копирование с помощью функции Сору:
> S:=Create((-irn/n!,ChebyshevT(n,x));
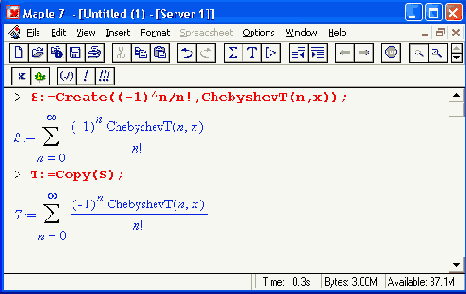
Вычисление производной от ряда с ортогональными многочленами представлено ниже:
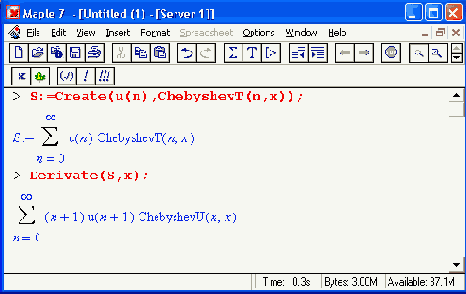
Еще один пример демонстрирует операцию скалярного умножения ряда с помощью функции ScalarMultiply:

Приведенные примеры показывают, что применение этого пакета достаточно просто. С деталями (порой довольно многочисленными) применения функций этого пакета можно познакомиться по справке на данный пакет.
Пакет для работы с симметрией Ли liesymm
В этом пакете, являющемся реализацией алгоритма Харрисона-Эстабрука, имеется ряд функций:
> withCllesymm);
Warning, the protected name close has been redefined and unprotected
[ c£A,&mod, H,Lie, Lrank, TD, annul, autosimp, close, d, depvars, determine, dvalue, extgen, extvars, getcoeff, getform, hasclosure, hook, indepvars, makeforms, mixpar, prolong, reduce, setup, translate, vfix, wcollect, wdegree, wedgeset, wsubs]
Эти функции достаточно специфичны и могут пригодиться лишь узким специалистам.
Пакет для работы с таблицами Spread
Загрузка этого пакета дает средства для работы с таблицами:
> with(Spread);
{CopySelection, CreateSpreddsheet,, EvaluateCurrentSelection, EvahiateSpreadsheet,
GetCellFormula, GetCellVabe, GetFormulaeMatrix, GetMaxCok, GetMaxRows, GetSelection, GetValuesMatrix, lnsertMatrixIntoSelection , IsStale, SetCellFormula, SetMatrix, SetSelection]
Функции пакета не имеют самостоятельного значения и призвана поддерживать работу с электронными таблицами, которая уже была подробно описана. Они дают такие средства, как создание в документе шаблона таблиц, проведение операций по заполнению и редактированию ячеек таблиц, копированию содержимого таблиц в буфер памяти и т. д. Назначение функций достаточно очевидно из их составных имен.
Пакет для работы с тензорами tensor
Этот пакет впервые появился в реализации Maple V R5. Он дает средства для работы с тензорами и вычислениями, используемыми в общей теории относительности. В нем использован специальный тип данных tensor_type в виде таблиц с двумя полями: компонентов и характеристик индексов. Поле компонентов — массив с размерностью, эквивалентной рангу объекта. Поле характеристик индексов задается списком чисел 1 и -1. При этом 1 на i-й позиции Означает, что соответствующий индекс контрвариантный, а -1 — что он ковариантный.
Процедура tensor_type возвращает логическое значение true, если ее первый аргумент удовлетворяет свойствам тензора, и false, если он этому свойству не удовлетворяет.
Каждому тензору соответствуют еще две таблицы. Таблица коэффициентов вращения задает коэффициенты вращения Ньюмена—Пенроуза, которые вычисляются функцией tensor[npspin] и индексируются именами греческих букв alpha, beta, gamma, epsilon и т. д. Другая таблица (компонент кривизны) содержит компоненты кривизны Ньюмена—Пенроуза. Они представлены тремя полями: полем Phi в виде массива размерности (0..2.0..2) с компонентами Риччи, поле Psi с массивом размерности (0. .4) с компонентами Вейля и полем R со скаляром Риччи.
Объявление:
> with(tensor);
[Christoffell, Christoffel2, Einstein, Jacobian, Killing_eqns, LevijCivita, Lie_diff, Ricci, Ricciscalar, Riemann, RiemannF, Weyl, act, antisymmetrize, change_basis, commutator,
compare, conj, connexF, contract, convertNP, cov_diff,
create,dlmetric, d2metric, directional_diff, displayGR, display_allGR, dual, entermetric, exteriorjiiff, exterior_prod, frame,geodesic_eqns, get_char, get_compts,get_rank, init, invars, invert, lin_com, lower, npcurve, npspin, partial_diff, permute_indices, petrov, prod, raise, symmetrize, tensorsGR, transform}
дает доступ к следующим функциям пакета:
Christoffell — вычисление символов Кристоффеля первого рода; Christoffel2 — вычисление символов Кристоффеля второго рода; Einstein — возвращение тензора Эйнштейна; display_alJGR — описывает ненулевые компоненты всех тензоров и параметров, вычисленных командой tensorsGR (общая теория относительности); displayGR — описывает ненулевые компоненты конкретного тензора (общая теория относительности); Jacobian — Якобиан преобразования координат; Killng_eqns — вычисление компонентов для уравнений Киллинга (имеет отношение к симметриям пространства); LeviCivita — вычисление ковариантных и контрвариантных псевдотензоров Леви—Чивита; Lie_diff — вычисляет производную Ли тензора по отношению к контравариантному векторному полю; Ricci — тензор Риччи; Ricciscalar — скаляр Риччи; Riemann — тензор Римана; RiemannF — тензор кривизны Римана в жесткой системе отсчета; tensorsGR — вычисляет тензор кривизны в данной системе координат (общая теория относительности); Weyl — тензор Вейля; act — применяет операции к элементам тензора, таблицам вращений или кривизны; antisymmetrize — антисимметризация тензора по любым индексам; change_basis — преобразование системы координат; commutator — коммутатор двух контравариантных векторных полей; compare — сравнивает два тензора, таблицы вращений или кривизны; conj — комплексное сопряжение; connexF — вычисляет связующие коэффициенты для жесткой системы координат; contract — свертка тензора по парам индексов; convertNP — преобразует связующие коэффициенты или тензор Римана к формализму Ньюмена—Пенроуза; cov_diff — ковариантное дифференцирование; create — создает тензорный объект; dlmetric — первая частная производная метрики; d2metric — вторая частная производная метрики; directional_diff — производная по направлению; dual — осуществляет дуальную операцию над индексами тензора; entermetric — обеспечивает ввод пользователем координатных переменных и ковариантных компонент метрического тензора; externor_diff— внешнее дифференцирование полностью антисимметричного ковариантного тензора; exterior_prod — внешнее произведение двух ковариантных антисимметричных тензоров; frame — задает систему координат, которая приводит метрические компоненты к диагональной сигнатурной матрице (с положительными или отрицательными единицами); geodesic_eqns — уравнение Эйлера—Лагранжа для геодезических кривых; get_char — возвращает признак (ковариантный/контравариантный) объекта; getcompts — возвращает компоненты объекта; get_rank — возвращает ранг объекта; invars — инварианты тензора кривизны Римана (общая теория относительности); invert — обращение тензора второго ранга; lincom — линейная комбинация тензорных объектов; lower — опускает индексы; npcurve — компонента кривизны Ньюмена—Пенроуза в формализме Дебевера (общая теория относительности); npspin — компонент вращения Ньюмена—Пенроуза в формализме Дебевера (общая теория относительности); partial_diff — частная производная тензора; permute_indices — перестановка индексов; petrov — классификация Петрова тензора Вейля; prod — внутреннее и внешнее тензорные произведения; raise — поднятие индекса; symmetrize — симметризация тензора по любым индексам; transform — преобразование системы координат. Примеры применения этого пакета можно найти в справочной базе данных системы.Пакет представляет интерес для физиков-теоретиков, работающих в области общей теории относительности и ее приложений/Для них (но не для большинства пользователей) приведенные данные полезны и понятны.
 |
 |
 |
Пакет для работы со случайными объектами RandomTools
Пакет для работы со случайными объектами RandomTools служит для расширения базовых возможностей системы Maple 7 (для большинства пользователей и так вполне достаточных) в части генерации различных случайных объектов, таких как числа различных форматов, векторов, матриц, строковых символов, таблиц и т. д. Они образно названы Flavor (в буквальном переводе «букет (вина)»), что подчеркивает возможную сложность структуры создаваемых объектов.
Пакет представлен небольшим числом основных функций:
> with(RandomTools);
[AddFlavor, Generate, GetFlavor, GetFlavors, HasFlavor, RemoveFlavor]
Однако функции AddFlavor и Generate могут использоваться с внушительным набором типов случайных объектов:
| Choose |
complex |
exprseq |
float |
identical |
| Integer |
list |
listlist |
negative |
negint |
| Nonnegative |
nonnegint |
nonposint |
nonpositive |
nonzero |
| Nonzeroint |
polynom |
posint |
positive |
rational |
| Set |
structured |
truefalse |
Действие большинства из них вполне очевидно из названий. Основной функцией является функция генерации случайных объектов Generate(expr). Если тип объекта не задан (например, функцией AddFlavor), то использование функции Generate будет порождать сообщение об ошибке. Примеры применения функций представлены ниже:

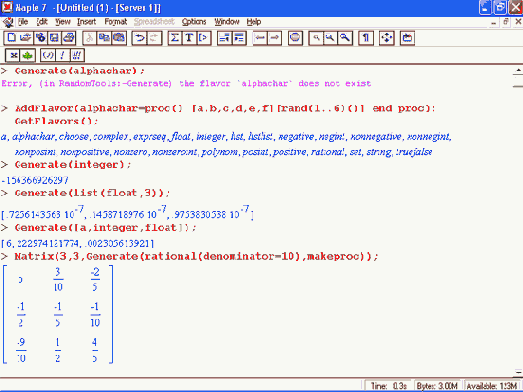
Функция GetFlavor(flvr) представляй случайный объект (или объекты) в форме процедуры:
> AddF1avor(a = rand(1..20)):
Generate(a):
15
> GetFlavor(a);
procO localt; global_seed;
_seed := irem(ax_seed,p);
t :=_seed;
toconcats do_seed:=irem(ax_seed,p);
t := sxt + _seed end do ;
irem(t, divisor) +offset endproc
> GetFlavor(integer);
module () localDefaults;
exportMain;
end module
Другая функция GetFlavors () возвращает все типы случайных объектов:
> GetFlavorsO;
a, alphachar, choose, complex, exprseq, float, integer, list, listlist, negative, negint, nonnegative, nonnegint, nonposint, nonpositive, nonzero, nonzeroint, polynom, posint, positive, rational, set, string, truefalse
Функция HasFlavor(flvr) служит для проверки наличия объекта данного типа в списке типов объектов, а функция RemoveFl avor(f1vr) — для удаления типа объекта. Следующие примеры иллюстрируют применение этих функций:
> HasFlavor(a):
true
> RemoveFlavor(a);
> HasFlavor(a):
false
> GetFlavors();
alphachar, choose, complex, exprseq, float, integer, list, listlist, negative, negint, nonnegative, nonnegint, nonposint, nonpositive, nonzero, nonzeroint, polynom, posint, positive, rational, set, string, truefalse
Обратите внимание на то, что после уничтожения объекта типа а он исчез из списка, выводимого функцией GetFlavors. Этот пакет, несмотря на довольно специфические возможности, наверняка будет полезен тем читателям, которые всерьез заняты реализацией «продвинутых» методов Монте-Карло, основанных на моделировании случайных объектов и ситуаций. Он служит серьезным дополнением к пакету статистических расчетов stats, описанному в этом уроке выше.
 |
 |
 |
Пакет для работы со списками ListTools
Новый пакет ListTools содержит ряд полезных команд для работы со списками. Их набор представлен ниже:
> with(ListTools):
Warning, the assigned name Group now has a global binding
[BinaryPlace, BinarySearch, Categorize, DotProduct, FindRepetitions, Flatten, FlattenOnce, Group, Interleave, Join, JoinSequence, MakeUnique, Pad, PartialSums, Reverse, Rotate, Sorted, Split, Transpose ]
Пакет содержит набор известных функций для работы со списками, например скалярного умножения списков, их обращения, транспонирования, поворота, объединения и т. д. Ограничимся примером на вычисление скалярного произведения векторов:
> L := [0., .84, .91, .14, -.76, -.96, -.28, .66, .99, .41, -.54]:
L := [0., .84, .91, .14, -.76, -.96, -.28, .66, .99, .41, -.54]
> М := [1., .54, -.42, -.99, -.65, .28, .96, .75, -.15, -.91, -.84];
М:= [ 1., .54, -.42, -.99, -.65, .28, .96, .75, -.15, -.91, -.84]
> DotProduct(L, L):
5.0063
> DotProduct(L, M):
.3162
Другие новые пакеты, CurveFitting и LinearFunctionalSystem, мы рассмотрели ранее достаточно подробно (см. уроки 14 и 15). В целом надо отметить, что состав пакетов Maple 7 существенно расширен по сравнению с предшествующими версиями системы. В то же время все пакеты, вошедшие в состав Maple 6, сохранены в новой версии программы — Maple 7, что гарантирует полную совместимость с ней. Практически это было подтверждено проверкой всех (а их многие сотни) примеров применения системы Maple 6 применительно к новой версии Maple 7.
Пакет Domains
Этот небольшой пакет служит для создания доменов — таблиц операций для вычислений. При его загрузке появляется сообщение о переопределениях объектов и список из всего лишь шести функций:
>restart;with(Domains):
Domains version 1.0
Initially defined domains are Z and Q the integers and rationale Abbreviations, e.g. DUP for DenseUnivariatePolynomial, also made Warning, the protected names Array, Matrix and Vector have been redefined and unprotected [Array, Matrix, Matrixlnverse, Vector, init, show]
Пакет допускает применение следующих конструкций:
Domains[domain] Doma1ns[evaldomains]
Domains[example] Domains[coding]
Приведенный ниже пример поясняет создание и использование доменов Q (для рациональных
данных) и Z (для целочисленных данных):
> Q['+'](l/2,2/5,3/8);
51/40
> Z[Gcd](660,130);
10
Следующая операция показывает, что домен Z является таблицей:
> type(Z,table);
true
А функция show позволяет вывести полный перечень всех операций, доступных для домена Z:
> show(Z,operations);
Signatures for constructor Z'
note: operations prefixed by -- are not available
*: (Integers,Z) ->Z
* :(Z,Z*) ->Z
+ :(Z,Z*) ->Z
-: (Z,Z) -> Z'
- :Z ->Z
0:Z
1:Z
< :(Z,Z) -> Boolean
<= : (Z.Z) -> Boolean
<> : (Z.Z) -> Boolean
=:(Z.Z) -> Boolean
>: (Z.Z) -> Boolean
>-: (Z.Z) -> Boolean
Abs : Z ->Z
Characteristic : Integers
Coerce : Integers-> Z
Div : (Z.Z) -> Union(Z,.FAIL)
EuclideanNorm : Z -> Integers
Factor : Z -> [Z,.[[Z,Integers]*]]
Gcd : Z* -> Z
Gcdex : (Z,Z,Name) ->Z
Gcdex : (Z,.Z,Name,Name) -> Z
Input : Expression -> Union(Z,.FAIL)
Inv : Z -> Union(Z,FAIL)
Lcm : Z* -> Z
Max : (Z,Z*) -> Z
Min : (Z,.Z*)-> Z
Modp : (Z,.Z) ->Z
Mods : (Z.Z)--> Z
ModularHoraomorphlsm : () -> (Z -> Z.Z)'
Normal : Z -> Z
Output : Z -> Expression
Powmod : (Z,Integers,Z) -> Z
Prime : Z -> Boolean
Quo : (Z,.Z,Name) ->Z
Quo : (Z,.Z) -> Z
Random : О ->Z
RelativelyPrime : (Z,.Z) -> Boolean'
Rem : (Z,.Z,.Name)-> Z
Rera : (Z,Z) -> Z
Sign : Z -> UNIONU,.-l,0)
SmallerEuclideanNorm : (Z,.Z) -> Boolean
Sqrfree : Z ->[Z,.[[Z,.Integers]*]]
Type : Expression -> 'Boolean'
Unit : Z -> Z
UnitNormal : Z -> [Z,.Z,.Z]
Zero : Z -> Boolean
^ : (Z,Integers) -> Z.
Домены позволяют передавать в качестве параметра процедур набор функций в виде единого целою, что и объясняет название этих объектов. Предполагается, что это может привести к заметному сокращению кодов программ вычислений в будущих реализациях системы Maple. Пока же возможности доменов скорее выглядят как очередная экзотика, чем как реальное средство для оптимизации вычислений. Потребуется время, чтобы показать, что это не так.
 |
 |
 |
Пакет функций дифференциальных форм difforms
В пакете дифференциальных форм содержится следующий ряд функций:
> with(difforms);
[&^, d, defform,formpart,parity, scalarpart, simpform, wdegree]
Демонстрационные материалы по применению этого пакета входят в поставку Maple 7.
Пакет функций теории чисел numtheory
В этом обширном пакете собрано 46 функций, относящихся к теории чисел:
> with(numtheory);
Warning, the protected rame order has been redefined and unprotected
[GIgcd, bigomega, cfrac, cfracpol, cyclotomic, divisors ;factorEQ,factorset,fermat, imagunit, index, integral_basis, invcfrac, invphi, issqrfree,jacobi, kronecker, Я,legendre, mcombine, mersenne, minkowski, mipolys, mlog, mobius, mroot, msqrt, nearestp, nthconver, nthdenom, nthnumer, nthpow, order,pdexpand, ф,n,pprimroot,primroot, quadres, rootsunity, safeprime, o,sq2factor, sum2sqr, т,thue ]
В новой реализации Maple 7 число функций было уменьшено. Большинство функций этого пакета достаточно просты и заинтересовавшийся читатель вполне в состоянии провести их тестирование самостоятельно.
Пакет генерации кодов codegen
Пакет codegen представляет собой набор команд, предназначенных для организации взаимодействия системы Maple 7 с другими программными средствами:
> with(codegen);
[С, GRAD, GRADIENT, HESSIAN, JACOB1AN, cost, declare, dontreturn, eqnjortran, homer, intrep2maple,joinprocs, makeglobal, makeparam, makeproc, makevoid, maple2intrep, optim ize, packargs, packlocals, packparams, prep2trans, renamevar, split, swapargs ]
Этот пакет очень полезен программистам, занимающимся разработкой сложных программных комплексов. Пакет позволяет создавать процедуры на языке Maple 7 и транслировать их в программные модули, записанные на других языках программирования, таких как Фортран или Си.
Пакет ХМLTools
В Maple 7 резко расширены средства интеграции с Интернетом. Это сделано не только на уровне специфических для математических приложений средств, таких как рассмотренный выше пакет MathML, но и на уровне обычных языков сети, таких как HTML и XML.
Пакет XMLTools служит для поддержки средств языка XML. Этот пакет предоставляет весьма внушительное число функций для этого:
> with(XMLTools):
[AddAttribute, AddCfiild, AttrCont, AttributeCount, AttributeNames, AttributeValue, AttributeValueWithDefault, Attributes, CData, CDataData, CleanXML, Comment,
CommentText, ConfentModel, ContentModelCount, Element,
ElementName, ElementStatistics,Equal, FirstChild, FromString, GetAttribute, GetChild, HasAttribute, HasChild,
IsCData, IsComment, IsElement, IsProcessinglnstruction,
IsTree, JoinEntities, LastChild, MakeElement, Print, PrintToFile, PrintToString, ProcessAttributes, ProcessingInstruction, ProcessinglnstructionData, ProcessinglnstructionName, ReadFile, RemoveAttribute, RemoveAttributes, RemoveChild, RemoveContent, SecondChild, Select Attributes, SelectContent, SelectRemoveAttributes, SelectRemoveContent, SeparateEntities, Serialize,
Strip Attributes, StripComments, SubsAttribute, SubsAttributeName, ThirdChild, ToString, WriteFile]
Рассмотрение этих средств (как и средств поддержки HTML) далеко выходит за пределы тематики данной книги, хотя многие из них достаточно просты. Поэтому ограничимся единственным примером применения функции Print для получения программы на языке XML соответствующей программе задания выражения, рассмотренного в предшествующем разделе:
> XMLTools[Print](К );
<math xmlns='http://www.w3.org/1998/Math/MathML1>
<semantics>
<mrowxref='id5'>
mrowxref='id3'>
<mixref='idl'>a</mi>
<mo>⁢</mo>
<mixref='id2'>x</mi>
</mrow> <mo>+</mo>
<mixref='ld4'>b</m1>
</mrow>
<annotation-xml encoding='MathML-Content'>
apply id='id5'>
<plus/>
<apply id='id3'>
<times/>
<ci id='idl'>a</ci>
<ci id='id2'>x</ci>
</apply>
<cild='id4'>b</ci>
</apply>
</annotation-xml>
<annotat1on encoding='Maple'>a*x+b</annotation>
</semantics>
</math>
 |
 |
 |
Пакет команд для решения уравнений SolveTools
Пакет команд с весьма многообещающим названием SolveTools на самом деле содержит вовсе не средства для решения уравнений, а несколько весьма специфических функций:
> with(SolveTools):
[Basis, Complexity, GreaterComplexity, RationalCoefficients, SortByComplexity]
Функции этого пакета позволяют найти базис выражений, дескрипторы и рациональные коэффициенты. Примеры применения этого пакета очень просты, и с ними несложно ознакомиться. Однако при этом возникает вопрос «Зачем это надо?», который (увы!) остается без ответа.
Пакет линейных операторов Linear-Operators
Пакет линейных операторов LmearOperators — новый пакет, содержащий средства для работы с линейными операторами. Состав пакета виден из его вызова:
> with(LinearOperators);
[Apply, DEToOrePoly, FactoredAnnihilator, FactoredGCRD,
FactoredMinimalAnnihilator,FactoredOrePolyToDE, FactoredOrePolyToOrePoly, FactoredOrePolyToRE, IntegrateSols, MinimalAnnihilator, OrePolyToDE, OrePofyToRE, REToOrePoly, dAlembertianSolver}
Набор функций пакета достаточно представителен. Но, поскольку область применения пакета весьма специфична, рекомендуется знакомиться с его возможностями по справкам на его функции и обзорной статье по нему, имеющейся в обзоре новых пакетов расширения Maple 7 (также размещенной в справочной базе данных пакета).
Пакет операций для работы с конечными группами group
Этот пакет содержит довольно представительный набор функций для работы с конечными группами:
> with(group);
[DerivedS, LCS, NormalClosure, RandElement, SnConjugates, Sylow,areconjugate, center,
centralizer, core, cosels, cosrep, derived, elements,groiipmember,grouporder, inter, invperm, isabelian, isnormal,issubgroup, mulperms, normalizer, orbit, parity,
permrep, pres, transgroup ]
Функции этого пакета представляют интерес для математиков, работающих в области конечных групп. Но вряд ли они будут полезны большинству пользователей. Тем не менее, наличие таких функций говорит о полноте функциональных возможностей системы Maple 7.
Пакет организации многопроцессорной работы process )
Этот узкоспециализированный пакет содержит ряд функций по организации работы на нескольких процессорах:
> with(process):
[block, ey.ec, fork, kill, pclose, pipe, popen, wait ]
Данные функции представляют интерес для пользователей операционной системы UNIX, так что в проблематику данной книги не входят.
Пакет поддержки стандарта MathML
Для представления математической информации на страницах Интернета в последние годы был создан специальный язык MathML. Пока для большинства пользователей MathML — просто «экзотика», но так как наряду с XML его поддерживает World Wide Web Consortium, его вынуждены поддерживать все солидные фирмы — причем не только создающие системы Компьютерной математики. Среди них такие крупные корпорации, как Intel, IBM и Microsoft. В Maple 7 предусмотрена новая возможность поддержки стандарта MathML 2.O. Для такой поддержки используются MathML Viewer (см. урок 2) и пакет MathML.
Пакет MathML дает минимальный набор функций для использования языка MathML:
> with(HathML);
[Export, ExportContent, ExportPresentation, Import, ImportContent]
В нем всего 5 функций, что позволяет разобрать их достаточно детально. Первые три функции служат для экспорта выражений:
Export(expr) — преобразует Maple-выражение ехрr в параллельное MathML-выражение; ExportContent (expr) — преобразует Maple-выражение ехрr в MathML-выра-жение в формате содержания; ExportPresentation (ехрr) -преобразует Maple-выражение expr в MathML-выражение в формате представления.Еще две функции служат для импорта строки в формате MathML и его преобразования в Maple-выражение:
Import(mnlstring) и ImportConterrt(mmlstnng)
Следующий пример наглядно иллюстрирует применение функций пакета расширения MathML для преобразования математического выражения а*х+b вначале в запись на MathML, а затем преобразование этой записи str в Maple-выражение:
> str:=MathML[Export]
( а*х + b );
str := "<math xmlns-http://www.w3.org/1998/Math/MathML'> <semanticsXmrow xrfe f='id5'xmrow xref='id3'xnii xref='idl '>a</mi><mo>⁢</moXml xref='id2'>x</mi></mrowxmo>+</mo><mixref='id4'>b</mi>
</mrowXannotati on-xml encodrag='MathML-Content'><apply id='id5'><plus/><apply id='id3'xtft mes/xci id='idl'> a</ci><ci id='id2'>x</cix/applyxci id='id4'>b</ci></apply>\ </annotation-xml> <annotationencoding='Maple'> a*x+b </annotationx/semantics\ ></math>" > Import(str):a x + b
Этот пример показателен тем, что дает представление о виде записей на языке MathML. Нетрудно заметить, что это достаточно громоздкий язык. Функции, представленные выше, автоматизируют процесс составления записей на языке MathML обычных математических выражений, что делает доступной для обычных пользователей подготовку публикации в Интернете, содержащей математические выражения.
Пакет поддержки вычислений с размерными величинами Units
При выполнении большинства вычислений рекомендуется использовать безразмерные величины. Однако в некоторых областях науки и техники, например в физике, широко используются размерные величины, у которых помимо их значения указываются единицы измерения. Довольно развитую поддержку таких расчетов обеспечивает новый пакет расширения системы Maple 7 — Units. Он содержит следующие функции:
> with(Units);
[AddBaseUnit, AddDimension,AddSystem, AddUnit, Converter, GetDimension, GetDimensions, GetSystem, GetSystems, GetUnit, GetUnits, HasDimension, HasSystem, HasUnit, Natural, RemoveDimension, RemoveSystem, Standard, Unit, UseContexts, UseSystem, UsingContexts, UsingSystem]
Большинство функций этого пакета достаточно просты и даже очевидны. В связи с этим ограничимся несколькими характерными примерами их применения:
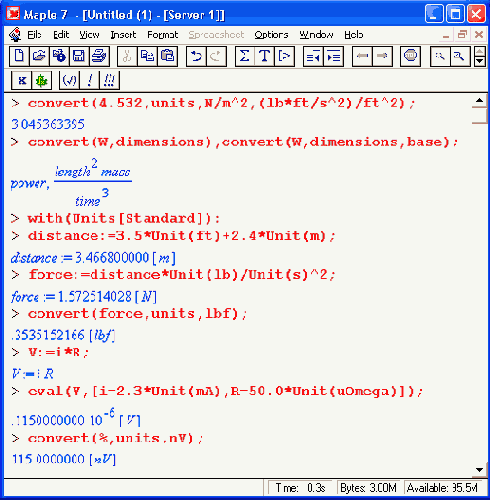
Пакет создания контекстных меню context
Пакет context служит для создания контекстных меню. Он содержит небольшое число функций:
> with(context):
[buildcontext, clearlabels, defaultcontext,
display, installcontext, restoredefault,
testactions, troubleshoot]
Этот пакет используется довольно редко и в основном пользователями, решающими в среде Maple не вычислительные, а системные задачи. Описание таких задач выходит за рамки данной книги.
Пакет создания внешних программ ExternalCalling
Пакет ExternalCalling служит для создания внешних программ, записанных на языке Maple (или C++). Состав пакета представлен небольшим числом функций:
DefineExternal(fn,extlib) — используя функцию define_external, Maple 7 задает внешнюю функцию fn в таблице функций внешних библиотек extlib; External LibraryName (basename, precision) — задает имя basename функции и точность вычислений precision для функции внешней библиотеки.Детальное знакомство с этим пакетом мы опускаем. Заинтересованный читатель найдет нужные сведения в справке по этому пакету.
Получение информации о графе
Еще один пример, приведенный ниже, иллюстрирует работу функции show, выдающей таблицу с полной информацией о графе, созданном функцией complete:
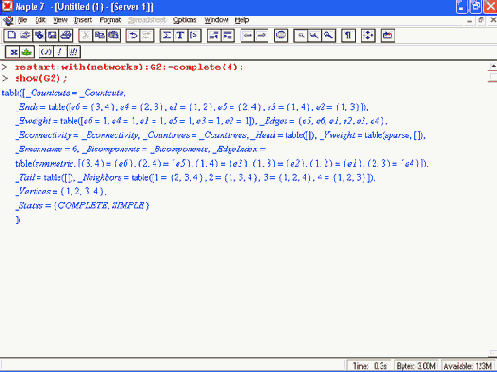
Разумеется, приведенные примеры далеко не исчерпывают всех задач, которые можно решать с применением графов. Но они наглядно демонстрируют, что для большинства пользователей пакет networks превращает графы из окутанного ореолом таинственности модного средства в простой рабочий инструмент.
Построение алгебраических кривых класса knot
Функция plot_knot позволяет строить одну или несколько алгебраических кривых — узлов. Пример построения целого семейства узлов показан на рис. 16.7.
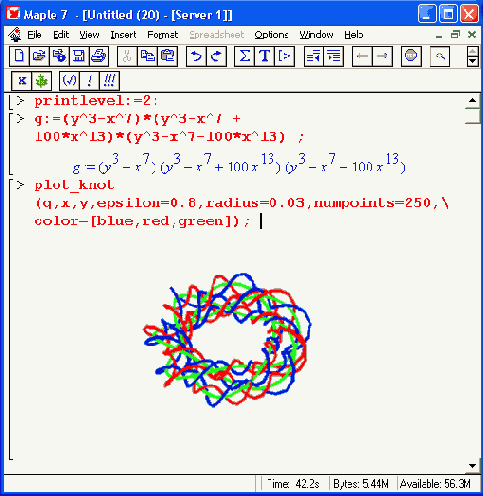
Рис. 16.7. Семейство узлов
Для лучшего обзора таких кривых рекомендуется воспользоваться возможностью вращения трехмерных фигур мышью для уточнения угла, под которым рассматривается фигура — в нашем случае семейство алгебраических кривых. Построение на рис. 16.7 выполняется довольно медленно — даже на компьютере с процессором Pentium III 600 МГц оно занимает около минуты.
Пример применения пакета geom3d
Учитывая сказанное, ограничимся единственным примером применения этого пакета (рис. 16.6).
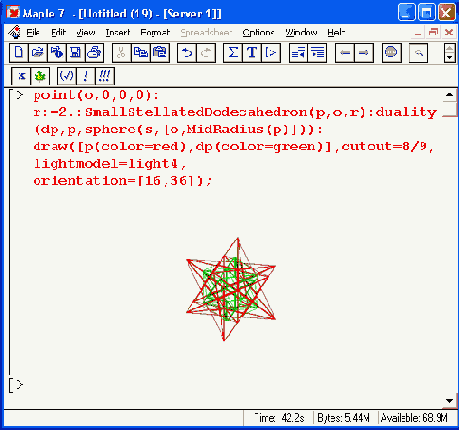
Рис. 16.6. Иллюстрация применения пакета geom3d
Напоминаем, что цель пакета не в построении рисунков геометрических фигур, а в аналитическом представлении объектов в пространстве. Поэтому в обширной базе данных справочной системы по этому пакету вы встретите очень много рисунков.
Пример применения расчетных функций пакета geometry
К сожалению, описание всех функций этого пакета потребует привести справочные данные практически по всей геометрии на плоскости, объем которых намного превышает объем данной книги. Учитывая идентичность идеологии при работе с функциями этого пакета, большинство из которых имеет вполне прозрачные имена (правда, англоязычные), работу с пакетом поясним на примере одной из функций — circle. Она позволяет математически задать окружность и определить все ее геометрические параметры. Функция может иметь несколько форм записи. Например, в форме:
circle(c,. [А. В. С], n, 'centername'=m)
она определяет построение окружности, проходящей через три точки А, В и С. Необязательный параметр n — список с именами координатных осей. Параметр ' centername' =m задает имя центра.
В форме circle(c. [А. В], n, 'centername'=m) задается окружность, проходящая через две точки А и В, а в форме circle(c, [A, rad], n, 'centername'=m) задается окружность, проходящая через одну точку А с заданным (и произвольным) радиусом rad и центром с. Наконец, функция circle в форме circle (с, eqn, n, 'centername'=m) позволяет задать окружность по заданным уравнению eqn и центру с. Проиллюстрируем применение функции circle на следующих примерах. Зададим характеристические переменные:
> EnvHorizontalName := m: _EnvVertlcalNane :=n;:
Определим окружность c1, проходящую через три заданные точки А, В и С с указанными после их имен координатами, и найдем координаты центра этой окружности:

Далее найдем радиус окружности:

и уравнение окружности, заданное в аналитическом виде:
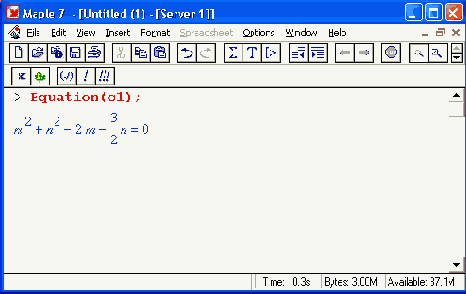
Наконец, с помощью функции detail получим детальное описание окружности:

Заинтересованный в таких расчетах читатель может самостоятельно ознакомиться с другими функциями аналогичным образом, тем более, что в справочной системе этого пакета имеется множество примеров работы с его функциями.
Примеры применения пакета algcurves
Приведем примеры применения функций пакета algcurves:

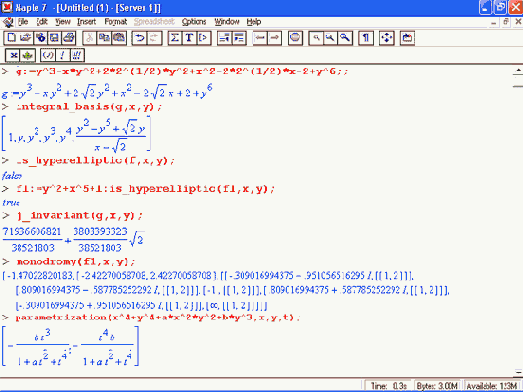
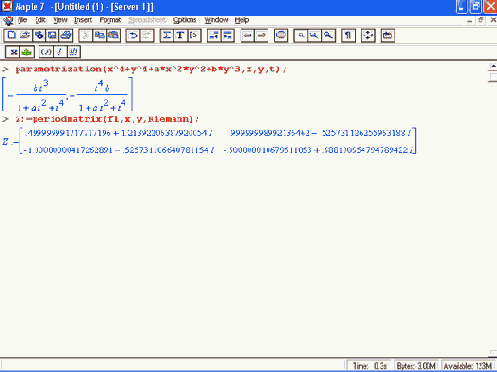
Примеры применения пакета networks
Рассмотрим некоторые избранные функции этого пакета, которые наиболее часто используются при работе с графами. Детали синтаксиса функций можно найти в справочной базе данных Maple 7.
Функции создания графов:
new — создает пустой граф (без ребер и узлов); void — создает пустой граф (без ребер); duplicate — создает копию графа; complete — создает полный граф; random — возвращает случайный граф; petersen — создает граф Петерсена. Функции модификации графов: addedges — добавляет в граф ребро; addvertex — добавляет в граф вершины; connect — соединяет одни заданные вершины с другими; delete — удаляет из графа ребро или вершину. Функции контроля структуры графов: draw — рисует граф; edges — возвращает список ребер графа; vertices — возвращает список узлов графа; show — возвращает таблицу с полной информацией о графе; . ends — возвращает имена вершин графа; head — возвращает имя вершины, которая является головой ребер; tail — возвращает ими вершины, которая является хвостом ребер; incidence — возвращает матрицу инцидентности; adjacency — возвращает матрицу смежности; eweight — возвращает веса ребер; weight — возвращает веса вершин; isplanar — упрощает граф, удаляя циклы и повторяющиеся ребра, и проверяет его на планарность (возвращает true, если граф оказался планарным, и false — в противном случае).Функции с типовыми возможностями графов:
flow — находит максимальный поток в сети от одной заданной вершины к другой; shortpathtree — находит кратчайший путь в графе с помощью алгоритма Дейкстры.Каждая из этих команд имеет одну или несколько синтаксических форм записи. Их можно уточнить с помощью справочной системы. С ее помощью можно ознакомиться и с назначением других функций этого обширного пакета. Проиллюстрируем его применение на нескольких типичных примерах.
На рис. 16. 9 показан пример создания Графа, имеющего четыре вершины, и графа Петерсона с выводом их графиков графической функцией draw.
На рис. 16.10 показан другой пример работы с графами — построение графа функцией complete и затем его преобразование путем удаления части вершин. Исходный и преобразованный графы строятся функцией draw.
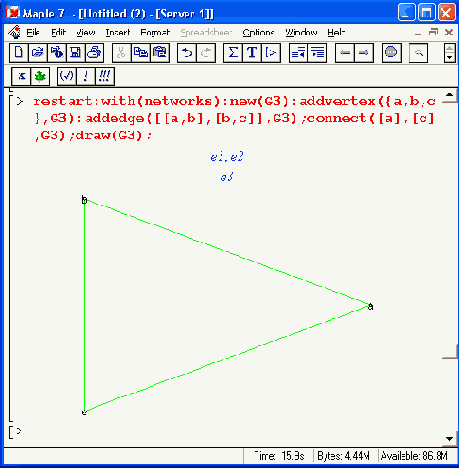
В третьем примере (рис. 16.11) граф формируется по частям — вначале задается пустой граф функцией new, а затем с помощью функций addvertex и addedge в него включаются вершины и ребра. Далее функция connect соединяет вершину а с вершиной с, делая граф замкнутым. Функция draw строит сформированный таким образом граф, а функции head и tail используются для выявления «голов» и «хвостов» графа.
В четвертом примере, представленном на рис.,16.12, показано создание графа G2 (его изображение было приведено на рис. 16.10) с вычислением для этого графа максимального потока от вершины 1. Обратите внимание, что в параметрах функции flow, использованной для этого, заданы две переменные: eset — принимает значение множества с ребрами, по которым проходит максимальный поток, и соmр — принимает значение множества, в котором содержатся вершины, по которым проходит максимальный поток. Значения этих переменных выведены в области вывода. В заключительной части этого примера показано применение функции shortpathtree, ищущей наиболее короткий путь от вершины 1 до других вершин.


Рис. 16.9. Построение графов
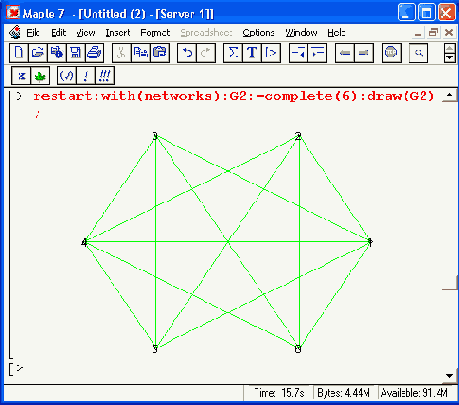

Рис. 16.10. Преобразование графа удалением части вершин

Прочие функции пакета simplex
Функция basis(C) возвращает базис для системы линейных уравнений С. Например:
> basisC [ х - 2*z+w , z - 2*у - w ] );
[x,z]
Функция convexhull(ps) возвращает выпуклую оболочку множества точек ps:
> convexhum{[0,0],[l,l],[2,-l],[1,1/3],[1,1/2]}):
[[0,0],[2,-1],[1, 1]]
Для определения констант для системы линейных уравнений или неравенств служит функция cterm(C):
> cterm([2*х+у<=6.7*y-z-3-4]);
[6,7]
Функция define_zero(C) возвращает ближайшее ненулевое значение, зависящее от установки переменной Digits:
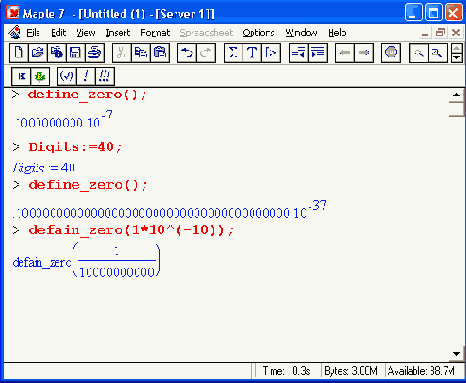
Функция display(C) имеет еще и форму display(C,[X, у, z]). Она задает вывод линейных уравнений и неравенств в матричной форме:

Функция dual(f, С, у) имеет следующие параметры: f — линейное выражение y, С множество неравенств и у — имя. Эта функция возвращает сопряженное с f выражение:
> dual( x-y,{2*x+3*y<=5.3*x+6*y<=15},z);
115zl +5z2, {1_<3z1+2z2,-l_<6z1+3z2}
Функция feasible может быть задана в трех формах:
feasible(C)
feasible(C,vartype)
feasible(C,vartype,'NewC','Transform')
Здесь параметр vartype может иметь значения NONNEGATIVE или UNRESTRICTED. Эта функция определяет систему как осуществимую или нет:
> feasible({2*x+3*y<-5, 3*x+6*y<"15}, NONNEGATIVE);
true
> feasib1e({2*x+3*y<-5, 3*х+б*у<—15}, NONNEGATIVE);
false
Если функция возвращает логическое значение true, то заданная система осуществима, а если false — неосуществима, то есть ни при каких значениях переменных не способна удовлетворить записанным неравенствам и равенствам. Функция pivot (С, х, eqn) конструирует новую систему с заданным главным элементом:
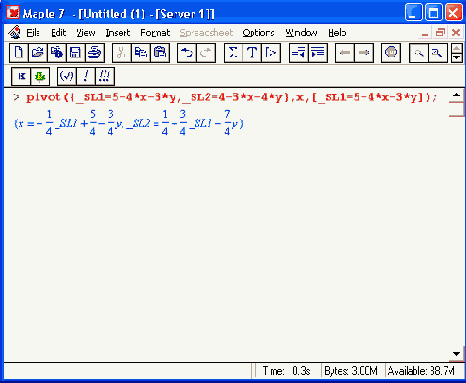
Функция pivoteqn(C, var) возвращает подсистему для заданного диагонального элемента С:
> pivoteqnC {_SL1 - 5-3*х-2*у. _SL2 - 4-2*х-2*у}. х );
[_SLl = 5-lx-2y]
Функция pivotvar(f, List) или pivotvar(f) возвращает список переменных, имеющих положительные коэффициенты в выражении для целевой функции:

Функция ratio(C, x) возвращает список отношений, задающих наиболее жесткие ограничения:
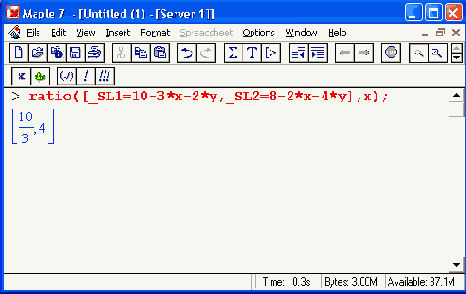
Функция setup может иметь три формы:
setup(C)
setup(C, NONNEGATIVE)
setup(C, NONNEGATIVE, 't')
Она обеспечивает конструирование множества уравнений с переменными в левой части:

Последняя функция — standartlze(C) — конвертирует список уравнений (неравенств) в неравенства типа «меньше или равно»:
> standardize({2*x+3*y<-5.3*x+5*yl5});
{2х + Зу<5,Зх + 5у<15,-Зх-5у<-15}
 |
 |
 |
Регрессионный анализ
Под регрессионным анализом (или просто регрессией) обычно подразумевают нахождение некоторой формальной аналитической зависимости, которая приближенно (по критерию минимума среднеквадратической ошибки) аппроксимирует исходную зависимость. Последняя чаще всего бывает представлена некоторым набором точек (например, полученных в результате эксперимента).
Для проведения регрессионного анализа служит функция fit, которая вызывается следующим образом:
stats[fit,leastsquare[vars,eqn.parms]](data)
или
fit[leastsquare[vars,eqn.parms]](data)
где data — список данных, vars — список переменных для представления данных, eqn — уравнение, задающее аппроксимирующую зависимость (по умолчанию линейную), parms — множество параметров, которые будут заменены вычисленными значениями.
На приведенных ниже примерах показано проведение регрессии с помощью функции fit для зависимостей вида у(х):
> with(stats):Digits:=5;
Digits := 5
> fit[leastsquare[[x,y]]]([[l,2,3,4].[3,3.5,3.9,4.6]]);
у = 2.4500 + .52000 х
>fit[leastsquare[[x,y], y=a*x"2+b*x+c]]([[l.2,3.4],[1.8,4.5,10,16.5]]);
2
у = .95000 х + .21000 х + .55000
В первом примере функция регрессии не задана, поэтому реализуется простейшая линейная регрессия, и функция fit возвращает полученное уравнение регрессии для исходных данных, представленных списками координат узловых точек. Это уравнение аппроксимирует данные с наименьшей среднеквадратичной погрешностью. Во втором примере задано приближение исходных данных степенным многочленом второго порядка. Вообще говоря, функция fit обеспечивает приближение любой функцией полиномом.
Рисунок 16.15 показывает регрессию для одних и тех же данных Полиномами первой, второй и третьей степени с построением их графиков и точек исходных данных. Нетрудно заметить, что лишь для полинома третьей степени точки исходных данных точно укладываются на кривую полинома, поскольку в этом случае (4 точки) регрессия превращается в полиномиальную аппроксимацию. В других случаях точного попадания точек на линии регрессии нет, но обеспечивается минимум среднеквадратической погрешности для всех точек — следствие реализации метода наименьших квадратов.
Функция fit может обеспечивать регрессию и для функций нескольких переменных. При этом надо просто увеличить размерность массивов исходных данных. В качестве примера ниже приведен пример регрессии для функции двух переменных:
>f:=fit[1eastsquare[[x,y,z],z=-a+b*x+c*y,{a,b,c}]]\
([[l,2,3.5,5],[2.4,6,8.8],[3,5,7,10,Weight(15,2)]]):
f:=z=l + 13/3x-7/6y
> fa:=unapply(rhs(f),x,y);
fa:=(x,y)->l + 13/3x-7/6y
z > fa(1.,2.);
2.999999999
>fa(2,3):
37/6
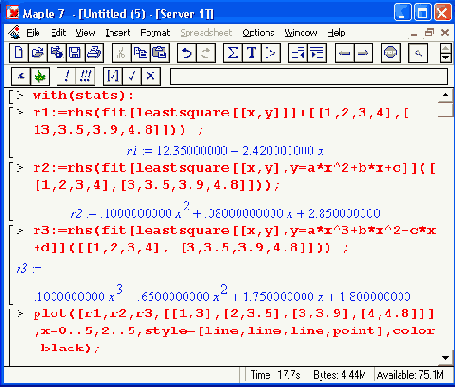

Рис. 16.15. Примеры регрессии полиномом и первой, второй и третьей степени
В данном случае уравнение регрессии задано в виде z = a + bx + cy. Обратите внимание на важный момент в конце этого примера — применение полученной функции регрессии для вычислений или построения ее графика. Прямое применение функции f в данном случае невозможно, так как она представлена в не вычисляемом формате. Для получения вычисляемого выражения она преобразуется в функцию двух переменных fa(x,y) путем отделения правой части выражения для функции f. После этого возможно вычисление значений функции fa(x,y) для любых заданных значений х и у:
К сожалению, функция fit неприменима для нелинейной регресии. При попытке ее проведения возвращается структура процедуры, но не результат регресии — см. пример ниже:
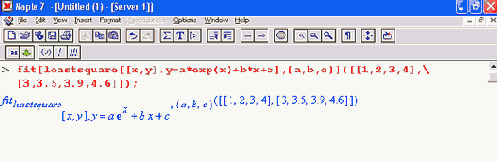
 |
 |
 |
Визуализация геометрических объектов с помощью пакета geometry
Одно из важных достоинств пакета geometry - возможность наглядной визуализации различных геометрических понятий, например графической иллюстрации доказательства теорем или геометрических преобразований на плоскости. Проиллюстрируем это на нескольких характерных примерах, заодно показывающих технику работы с рядом функций этого пакета.
Рисунок 16.1 показывает построение из множества окружностей фигуры - кардиоиды. Вопреки обычному построению этой фигуры, используется алгоритм случайного (но удовлетворяющего требованиям построения данной фигуры) выбора положений центров и радиусов окружностей.
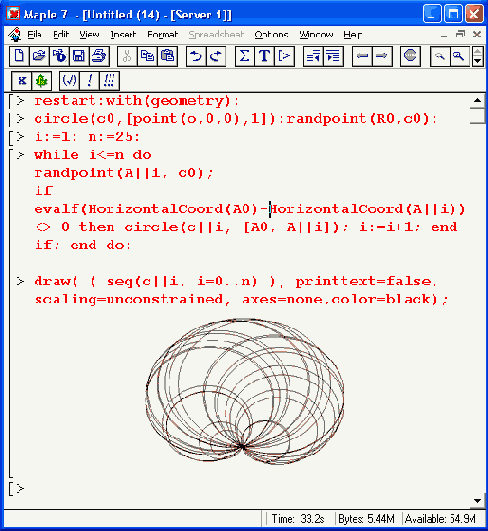
Рис. 16.1. Построение кардиоиды из окружностей
Рисунок 16.2 дает графическую иллюстрацию к одной из теорем Фейербаха. Здесь эффектно используются средства выделения геометрических фигур цветом, что, увы, нельзя оценить по книжной черно-белой иллюстрации.
На следующем рисунке (рис. 16.3) показано построение фигуры, образованной вращением множества квадратов относительно одной из вершин. Это хороший пример применения функций point, square,.rotation и draw из пакета geometry.
Рисунок 16.4 показывает гомологические преобразования квадрата. Заинтересовавшийся читатель может легко разобраться с деталями простого алгоритма этой программы.
ПРИМЕЧАНИЕ
Обратите особое внимание на последний параметр в функции draw. Он задает построение титульной надписи с заданными шрифтом и размером символов. Сравните титульные надписи на рис. 16.4 и 16.3, где титульная надпись сделана шрифтом, выбранным по умолчанию. Приятно, что в обоих случаях нет преград для использования символов кириллицы и создания надписей на русском языке.
Наконец, на рис. 16.5 показан пример построения трех окружностей, имеющих две общие точки. Обратите внимание на вывод надписей «о», «ol» и «о2», указывающих положение центров окружностей на рисунке.

Рис. 16.2. Графическая иллюстрация к теореме Фейербаха
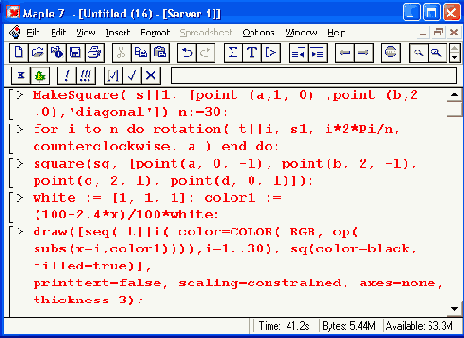
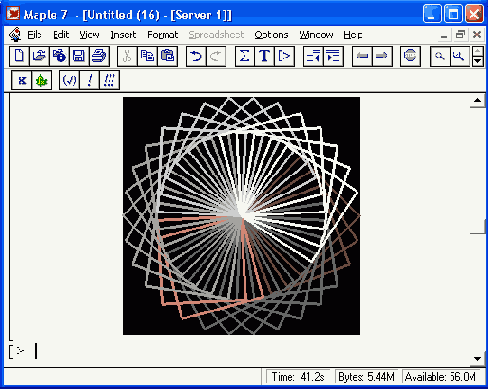
Рис. 16.3. Фигура, полученная вращением квадрата
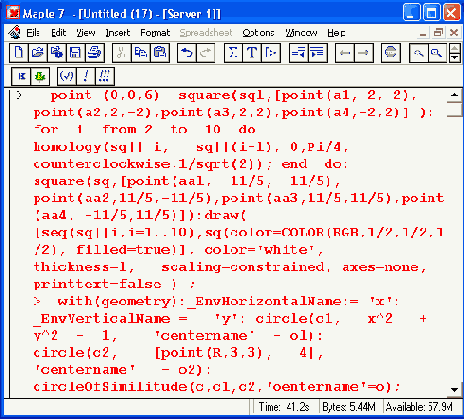
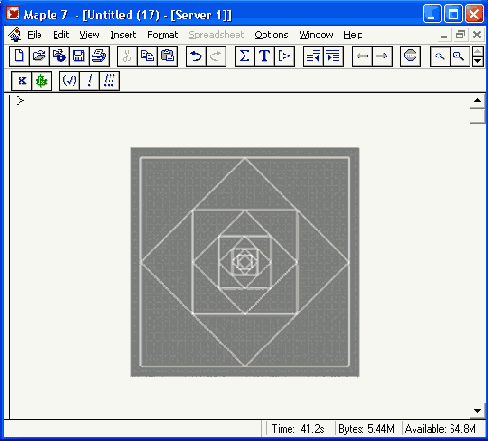
Рис. 16.4. Гомологические преобразования квадрата
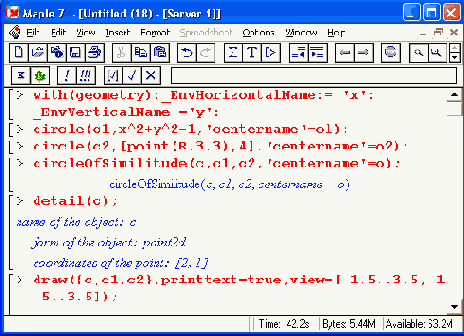
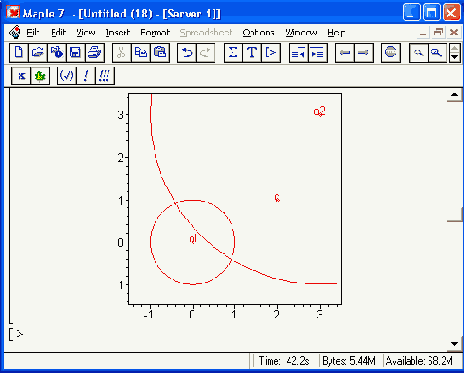
Рис. 16.5. Три окружности, имеющие две общие точки
Множество примеров применения всех функций пакета geometry дано в справочной системе Maple 7. Рекомендуется просмотреть те из них, которые нужны вам.
 |
 |
 |
Аппроксимации рядом Тейлора
Начнем с аппроксимации функции хорошо известным рядом Тейлора степени 8 относительно середины интервала (точки с х=2):

Такой ряд позволяет использовать для вычислений только арифметические действия, что само по себе здорово! Для удобства преобразуем аппроксимацию в функцию, чтобы она соответствовала форме, указанной для первоначальной функции f(x). Тогда мы сможем построить график кривой ошибок для аппроксимации полиномом Тейлора:

Кривая ошибок для аппроксимации полиномом Тейлора строится командой:
> plotd(f- TaylorApprox,0..4,.co1or=black);
и имеет вид, представленный на рис. 17.2. Эта кривая нас, прямо скажем, не слишком радует, поскольку погрешность в сотни раз превышает заданную.

Рис. 17.2. Кривая погрешности при аппроксимации рядом Тейлора
Типичное свойство аппроксимации рядом Тейлора состоит в том, что ошибка мала вблизи точки разложения и велика вдали от нее. В данном случае самая большая ошибка имеет место в левой оконечной точке. Чтобы вычислить значение ошибки в точке х =0, что ведет к делению на нуль (см. определение для f(x)), мы должны использовать значение предела:
> maxTaylorError := abs( Limit(f(x), х-0) - ТауlorАрргох(0) );
maxTaylorError := .0015029620
Итак, в самом начале наших попыток мы потерпели полное фиаско. Но отчаиваться не стоит, ибо, как говорят, «даже у хорошей хозяйки первый блин — комом».
Аппроксимация Чебышева-Паде
Теперь рассмотрим еще более точную рациональную аппроксимацию Чебышева-Паде. Это такая рациональная функция r[m, n](х) с числителем степени т и знаменателем степени п такой же, как и для разложения в ряд Чебышева. Функция r [m, n](х) согласуется с разложением в ряд Чебышева f(x) членом степени m+n. Мы вычислим аппроксимацию Чебышева-Паде степени (4,4), подобную обычной Паде- аппроксимации, успешно выполненной ранее:

Построим кривую ошибок:
> with(orthopoly, Т):
> plot(F = ChebPadeApprox, 0..4,color=black):
Она представлена на рис. 17.4.
Максимальная ошибка и на этот раз имеет место в левой оконечной точке. Величина максимальной ошибки несколько меньше, чем ошибка при аппроксимации рядом Чебышева. Главное преимущество представления в виде рациональной функции — высокая эффективность вычислений, которая может быть достигнута преобразованием в непрерывную (цепную) дробь (см. ниже). Однако полученная максимальная ошибка чуть-чуть больше заданной:
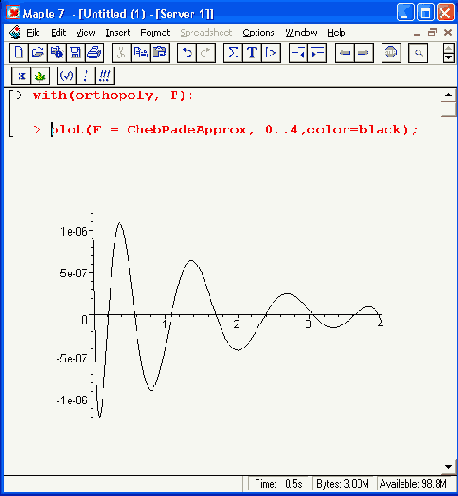
Рис. 17.4. Кривая ошибки при Паде-Чебышева рациональной аппроксимации
> maxChebPadeError :=abs( F(0) - ChebPadeApprox(O) );
maxChebPadeError= .1236746 10-5
Мы достигли впечатляющего успеха и остается сделать еще один шаг в направлении повышения точности аппроксимации.
Аппроксимация полиномами Чебышева
Знатоки техники аппроксимации знают, что лучшие приближения на заданном интервале могут быть получены при использовании разложения в ряд Чебышева. Это связано с тем, что ортогональные полиномы Чебышева позволяют получить аппроксимацию, погрешность которой в заданном диапазоне изменения аргумента распределена более равномерно, чем в предшествующих случаях. Выбросы погрешности на краях интервала аппроксимации в этом случае исключены.
Разложим функцию f(x) на [0, 4] в ряд Чебышева с точностью 1*10-8. Это означает, что все члены с коэффициентами меньше чем эта величина, будут опущены. Такая точность обеспечивается полиномом 13 степени:
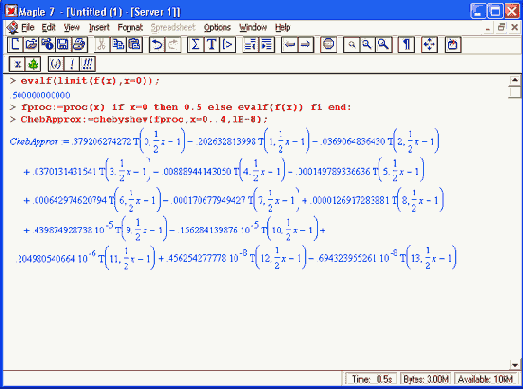
Можно проверить для этого примера, что кривая ошибки при аппроксимации рядом Чебышева колеблется. Поскольку ряд Чебышева был оборван на члене 8-й степени (как и полином ряда Тейлора), то максимальная ошибка оказалась равной приблизительно 0,6* 10-5. Эта величина уже на два порядка меньше, чем ошибка при Паде- аппроксимации, вычисленная выше. Но все же немного не дотягивает до наших требований.
Для последующих вычислений полезно заметить, что мы можем использовать процедуру для нахождения численных значений f(x), которая будет намного эффективнее, чем прямое определение, которое требует численного интегрирования для каждого значениях. А именно определим процедуру численной оценки, основанную на разложении в ряд Чебышева степени 13, так как максимальная ошибка при такой аппроксимации меньше чем 10~8, и обеспечивает для нашей цели достаточную точность. Мы определим полином Чебышева Т(х) из пакета orthopoly и затем для эффективной оценки преобразуем его в форму Горнера:
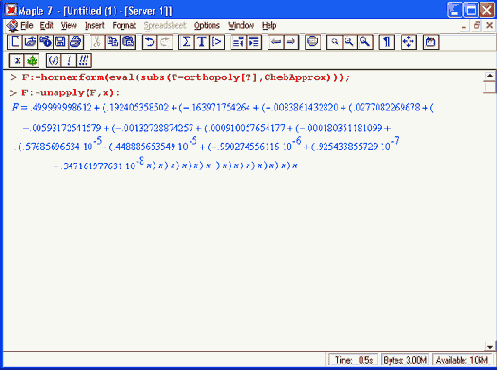
Схема Горнера минимизирует число арифметических операций, заменяя операции возведения в степень операциями последовательного умножения.
Движение частицы в магнитном поле
От реального мира перейдем к микромиру. Пусть микрочастица массой 9* 10-31 кг и зарядом +1,6*10"19 Кл влетает в магнитное поле с индукцией В = 0,1 Тл под углом а=80°. Рассчитаем траекторию движения частицы при начальной скорости Vo= 1*107м/с:
> restart;
Сила Лоренца, действующая на движущуюся частицу F = q*(E+[v, В]). Проекции векторного произведения [v, В] на оси х, у, z:
[v.B]x=vy*Bz-vz*By [v,B]y=vz*Bx-vx*Bz [v,B]z=vx*By-vy*Bz
В соответствии с этим известные из курса физики дифференциальные уравнения, описывающие траекторию полета частицы по осям х, у, z имеют вид:
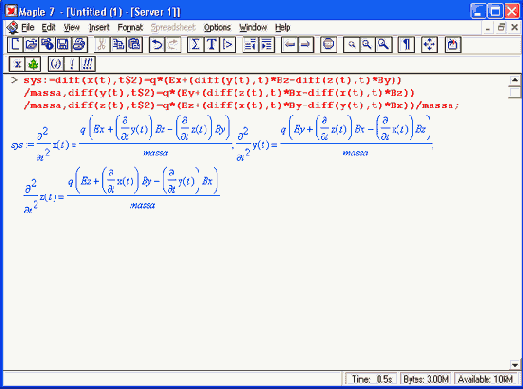
Зададим исходные числовые данные (опустив размерности):
> q:=-1.6e-19: massa:=9.1e-31: V:=le7: alpha:=80*Pi/180:
> Vx:=V*cos(alpha): Vy:=V*sin(alpha): Ex:=0:Ey:=0:Ez:=0: Bx:=0.1:By:=0: Bz:=0:
Построим траекторию движения частиц в пространстве:
> with(DEtools):DEplot3d({sys},{x(t),y(t),z(t)},t=0..2e-9, [[x(0)=O,D(x)(0)=Vx,y(0)==0,D(y)(0)=Vy,z(0)=0,D(z)(0)=0]], stepsize=le-ll,orientation=[24.117]):
Полученная траектория представлена на рис. 17.8. Она имеет вид спирали в пространстве. При этом скорость движения частицы вдоль оси х неизменна, а вдоль осей у и z имеет характерную колебательную компоненту. Случай явно куда менее тривиальный, чем полет камня, описанный выше.
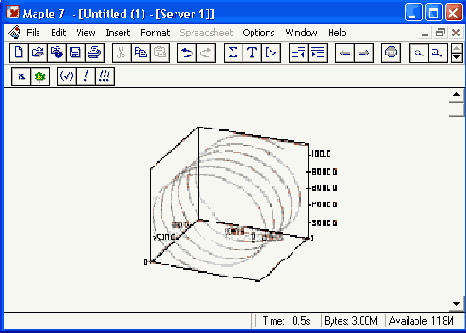
Рис. 17.8. Траектория движения частицы в магнитном поле
Мы можем найти аналитическое представление для траектории частицы в виде параметрически заданной (с параметром времени t) системы из трех уравнений:
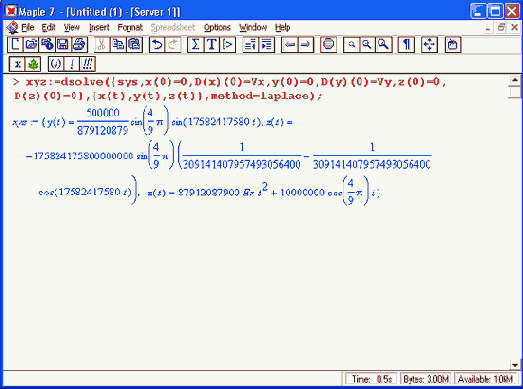
Моделирование движения заряженной частицы в пространстве с магнитным полем показывает, что для принятых для моделирования параметров решаемой задачи, движение частицы происходит по спиралеобразной траектории. Получен как график траектории движения частицы, так и аналитические уравнения, описывающие это движение.
Эффективная оценка рациональных функций
Полиномы числителя и знаменателя в минимаксной аппроксимации уже выражены в форме Горнера (то есть в форме вложенного умножения). Оценка полиномом степени п в форме Горнера при n-умножениях и n-суммированиях — это наиболее эффективная схема оценки для полинома в общей форме. Однако для рациональной функции степени (т, п) мы можем делать кое-что даже лучше, чем просто представить выражения числителя и знаменателя в форме Горнера. Мы можем нормализовать рациональную функцию так, что полином знаменателя будет со старшим коэффициентом, равным 1. Мы можем также заметить, что вычисление рациональной функции степени (т, п) в форме Горнера требует выполнения все m+n сложений , m+n-1 умножений и 1 деления. Другими словами, общий индекс действия есть:
m+n операций умножения/деления; m+n операций сложения/вычитания.Вычисление рациональной функции можно значительно сократить и далее, преобразуя ее в непрерывную (цепную) дробь. Действительно, рациональная функция степени (т, п) может быть вычислена, при использовании только:
max(m,n) операций умножения/деления; m+n операций сложения/вычитания.Например, если m = n, тогда эта новая схема требует выполнения только поло-, вины числа действий умножения/деления по сравнению с предшествующим методом. Для рациональной функции MlnimaxApprox вычисление в форме, выраженной выше, сводится к 9 действиям умножения/деления и 8 действиям сложения/вычитания. Число операций умножения/деления можно сократить до 8, нормализуя знаменатель к форме monic. Мы можем теперь вычислить непрерывную (цепную) дробь для той же самой рациональной функции. Вычисление по этой схеме, как это можно видеть из вывода Maple, сводятся только к 4 действиям деления и 8 действиям сложения/вычитания:
> MinimaxApprox := confracform(MinimaxApprox):
> lprint(MinimaxApprox(x));
-.468857770747е-1+1.07858705749/(х+4.41994843227+16.1901737091/ (х+4.29121842830+70.1948525272/(х-10.2912843004+ 4.77536150167/(х+1.23883665458))))
Малосигнальный анализ усилителя на полевом транзисторе
Рассмотрим классический усилительный каскад на полевом транзисторе, схема которого приведена на рис. 17.12, а. Его эквивалентная малосигнальная схема представлена на рис. 17.12, б.
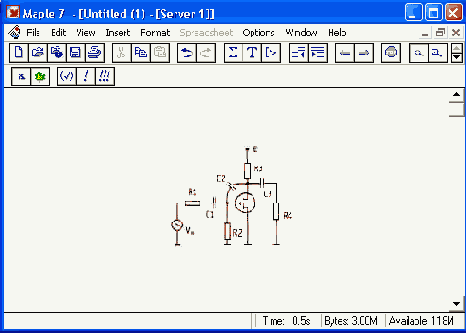
a
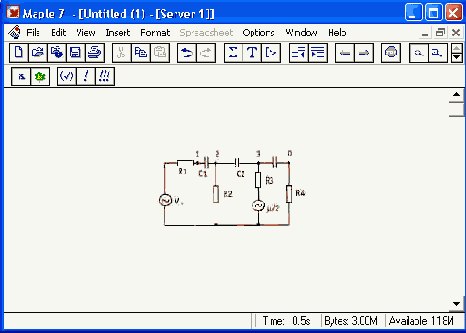
б
Рис. 17.12. Принципиальная (о) и эквивалентная(6) схемы усилителя на полевом транзисторе
Наша цель заключается в расчете характеристик усилителя операторным методом. Подключим нужный нам пакет plots:
> restart:with(plots):
Warning, the name changecoords has been redefined
Из законов Киргофа вытекает, что сумма токов, втекающих в каждый узел и вытекающих из него равна 0. Следовательно, для узлов эквивалентной схемы рис. 17.12 можно записать следующую систему уравнений в операторной форме:
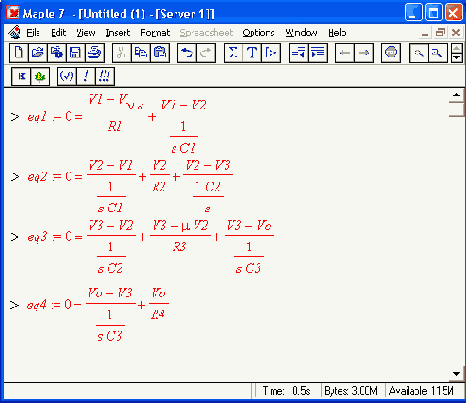
Переменные напряжения на узлах схемы находятся из аналитического решения данной системы. При этом заблокируем вывод их аналитических значений, поскольку он очень громоздок. Тем не менее вы можете посмотреть на полученные формулы, поставив знак точки с запятой вместо знака двоеточия в приведенных ниже выражениях:
> solve({eql,eq2,eq3.eq4}б{Vl,V2.V3,Vo}):
Обеспечим присвоение переменным Vo, VI, V2 и V3 найденных из решения системы уравнений значений:
> assign(%):
Теперь найдем операторную передаточную функцию в аналитическом виде:

В соответствии с выбранным операторным методом анализа введем обозначения:
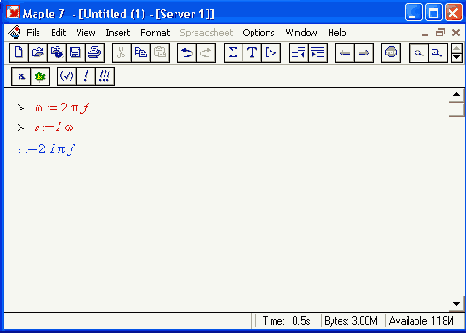
Это позволяет найти Н как функцию от частоты f также в аналитическом виде:
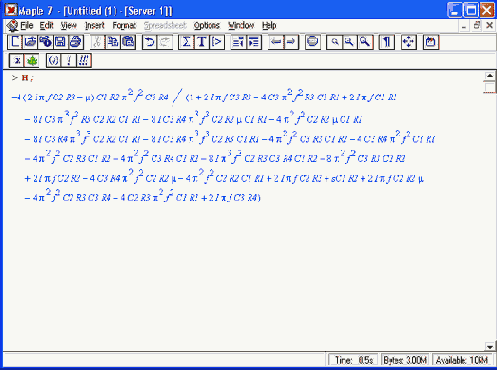
Это тоже довольно громоздкое выражение, и его применение при «ручном» анализе потребовало бы от нас немало изобретательности. Между тем Maple 7 позволяет «в два счета» определить из него амплитудно-частотную (AVM) и фазо- частотную (PhaseAV) характеристики усилителя как функции частоты:
> AVM=-evalc(abs(H)):
> PhaseAV:=evalc(argument(H)):
Преобразуем AVD в логарифмическую характеристику, выражающую усиление в децибелах (dB):
> AVdB:=20*1og10(AVM):
Такая характеристика более привычна для специалистов в радиоэлектронике. Соответственно фазо-частотную характеристику выразим в градусах:
> R2D:=evalf(360/(2*Pi));R2D := 57.29577950
> AVdeg:=R2D*PhaseAV:
Теперь можно перейти к обычным численным расчетам. Зададим конкретные значения компонент эквивалентной схемы усилителя:
> Rl:=100: R2:=100000: R3:=1000: R4:=10000: Cl:=1.*10^(-6): С2:=5*10^(-12): СЗ:=1*10^(-6): mu:=50:
Построим амплитудно-частотную характеристику усилителя:
> gaindata:-NULL:
phasedata:=NULL:
for a from 0 to 8 do:
for i from 2*10^a to l(T(a+l) by 10^a do
gaindata:=gaindata, [1. evalf(subs(f=i,AVdB))];
phasedata:=phasedata, [i, eva1f(subs(f=i,AVdeg))]:
od: od:
> 1oglogp1ot([gaindata]. thickness»2, color=black, style=1ine, axes=boxed,
title=`Коэффициент усиления K(f)`,1abels=['Частота (Hz)VK(d8)']):
Она показана на рис. 17.13.
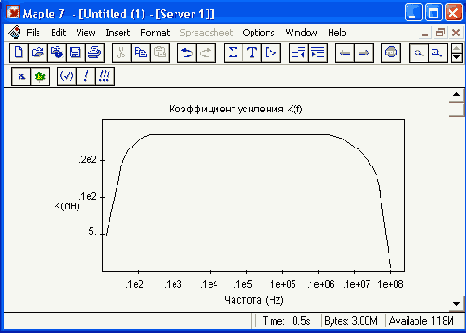
Далее зададим построение фазо-частотной характеристики усилителя:
> 1og1ogplot([phasedata], thickness=2, color=b1ue, style=line, axes=boxed, title='Фаэовый сдвиг (в градусах)`, labels=['Частота (Hz)','Фаза']);
Она представлена на рис. 17.14.
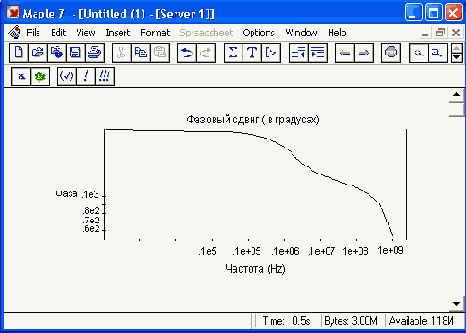
Найдем номинальный коэффициент усиления на частоте f=1000 (Гц):
> AVmid:=eva1f(subs(f=1000, AVdB)):
AVmid=33.12074854
Имея аналитическое выражение для амплитудно-частотной характеристики, можно составить уравнения для вычисления граничных частот (по спаду усиления на -dAV в dB):
> dAV:=3: #Ослабление (в dB на граничных частотах)
> eq5:=AVmid-dAV=20*log10(AVM):
Теперь можно найти эти частоты — нижнюю и верхнюю:
> flow:=fsolve(eq5,f. f-10..2000):flow:= 23.61659476
> fhigh:=fsolve(eqS,f, f-2000..100*10*6);
fliigh := .5737800225 107
Мы можем построить и более наглядную амплитудно-частотную характеристику с точками, соответствующими граничным частотам:
> with(plottools) :h:=log10(AVnvid-dAV):
aplot:= Loglogplot([gaindata], thickness=2, color=b1ack. style=line, axes=boxed,
title='Частоты flow и fhigh среза', labels=['Частота (Hz)VK(dB)']):
bplot:=line([0.1,h], [7.1,h], color=black, linestyle=3):
cplot:=line([log10(flow),0.58],[logHK flow). 1.6], color=blue, linestyle=3):
dplot:=line([log10(fh1gh).0.58],. [log10(fhigh).1.6],. color=red,. 1inestyle=3):
display([aplot.bplot,cplotJ,dplot]):
Эта характеристика показана на рис. 17.15.
На ней проставлены синяя и красная пунктирные вертикали, соответствующие найденным граничным частотам flow и fhigh, а также пунктирная горизонталь, соответствующая коэффициенту усиления на этих частотах. Это позволяет наглядно оценить частотный диапазон работы усилителя.
Таким образом, задача расчета усилителя в малосигнальном режиме полностью решена. Мы получили значение номинального коэффициента усиления, рассчитали нижнюю и верхнюю граничные частоты, получили аналитические выражения для амплитудно-частотной и фазо-частотной характеристик усилителя и построили их наглядные графики.
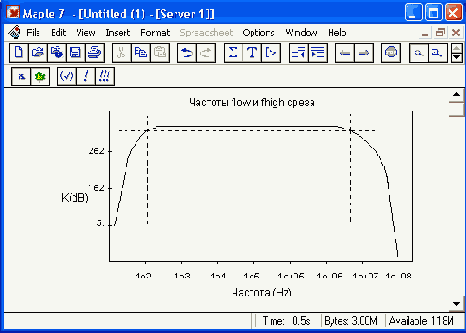
 |
 |
 |
Минимаксная аппроксимация
Классический результат теории аппроксимации заключается в том, что минимакс как наилучшая аппроксимация рациональной функции степени (т, п) достигается, когда кривая ошибки имеет m+n+2 равных по величине колебаний. Кривая ошибки аппроксимации Чебышева-Паде имеет нужное число колебаний, но эта кривая должна быть выровнена (по амплитуде выбросов кривой ошибки) с тем, чтобы обеспечить наилучшее минимаксное приближение. Эта задача решается с помощью функции minimax:

Максимальная ошибка в аппроксимации MinimaxApprox дается значением переменной maxerror. Заметим, что мы наконец достигли нашей цели получения аппроксимации с ошибкой меньшей, чем 1*10-6:
> maxMinimaxError := maxerror;
maxMinimaxError := .585025375366 10-6
Построим график погрешности для данного типа аппроксимации:
> plot(F = MinimaxApprox,0..4,color=black):
График ошибки, представленный на рис. 17.5, показывает равные по амплитуде колебания.
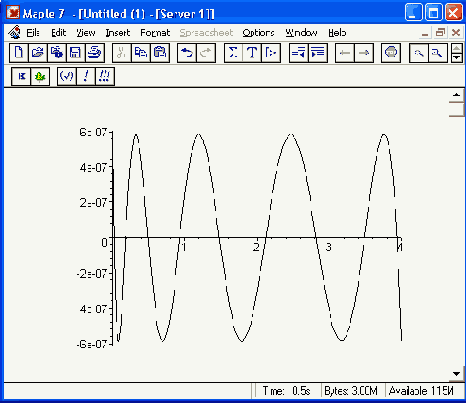
Рис. 17.5. График ошибки при минимаксной аппроксимации
Таким образом, мы добились блестящего успеха в снижении погрешности до требуемого и довольно жесткого уровня. Если бы мы задались целью получить только четыре или пять точных знаков аппроксимации, что в целом ряде случаев вполне приемлемо, то могли бы получить нужный результат гораздо раньше. Нам остается оптимизировать полученную аппроксимацию по минимуму арифметических операций и проверить реальный выигрыш по времени вычислений.
Моделирование цепи на туннельном диоде
А теперь займемся моделированием явно нелинейной цепи. Выполним его для цепи, которая состоит из последовательно включенных источника напряжения Es, резистора Rs, индуктивности L и туннельного диода, имеющего N-образную вольтамперную характеристику (ВАХ). Туннельный диод обладает емкостью С, что имитируется конденсатором С, подключенным параллельно туннельному диоду. Пусть ВАХ реального туннельного диода задана выражением:
> restart:
> A:=.3t: а:=10: В:=1*10^(-8): b:=20:
> Id:=Ud->A*Ud*exp(-a*Ud)+B*(exp(b*Ud-D):
Id:=Ud->AUde(-aUd)+Be(bUd-1)
Построим график ВАХ:
> plot(Id(Ud), Ud=-.02..0.76,color=black):
Этот график представлен на рис. 17.25. Нетрудно заметить, что ВАХ туннельного диода не только резко нелинейна, но и содержит протяженный участок отрицательной дифференциальной проводимости, на котором ток падает с ростом напряжения. Это является признаком того, что такая цепь способна на переменном токе отдавать энергию во внешнюю цепь и приводить к возникновению колебаний в ней различного типа.
Работа цепи описывается системой из двух дифференциальных уравнений:
di/dt=(Es-i(t)*Rs-u(t))/L
du/dt=(i(t)-Id(u(t))/C
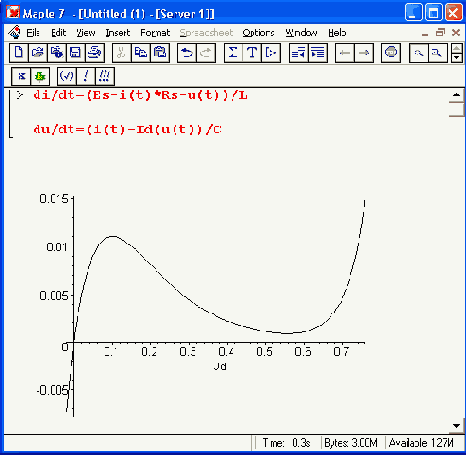
Рис. 17.25. ВАХ туннельного диода
Пусть задано Es = 0,35 В, Rs= 15 Ом, С = 10*10-12, L = 30*10-9 и максимальное время моделирования tm=10*10-9. Итак, задаем исходные данные:
> Es:=.35:Rs:=15:C:=10*10^(-12):L:=30*10^(-6):tm:=10*10^(-9):
Составим систему дифференциальных уравнений цепи и выполним ее решение с помощью функции dsolve:
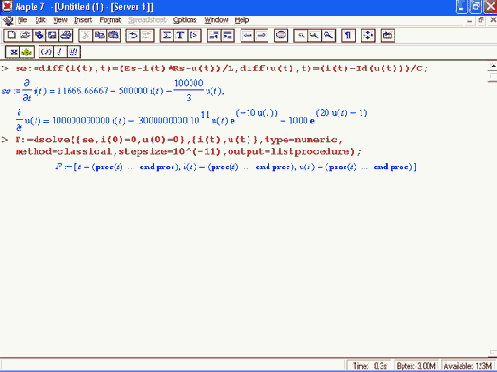
Поскольку заведомо известно, что схема имеет малые значения L и С, мы задали с помощью параметров достаточно малый шаг решения для функции dsolve — stepsize=l(T(-11) (с). При больших шагах возможна численная неустойчивость решения, искажающая форму колебаний, получаемую при моделировании. Используя функции odeplot и displ ay пакета plots, построим графики решения в виде временных зависимостей u(t) и 10*i (t) и линии, соответствующей напряжению Es источника питания:
> gu:=odeplot(F,[t,u(t)],0,tm,color=black,
labels=['tVu(t),10*i(tr]):
> gi:=odeplot(F,[t,10*i(t)],0..tm.color-black):
> ge:=odeplot(F,[t,Es].0..tm.color=red): .
> display(gu.gi,ge);
Эти зависимости представлены на рис. 17.26. Из них хорошо видно, что цепь создает автоколебания релаксационного типа. Их форма сильно отличается от синусоидальной.
Решение можно представить также в виде фазового портрета, построенного на фоне построенных ВАХ и линии нагрузки резистора Rs:
> gv:=plot({Id(Ud),(Es-Ud)/Rs},Ud=-.05..0.75,color=black,
labels=[Ud,Id]):
> gpp:=odeplot(F.[u(t),i(t)],0..tm,color=blue):
> display(gv,gpp);
Фазовый портрет колебаний показан на рис. 17.27.
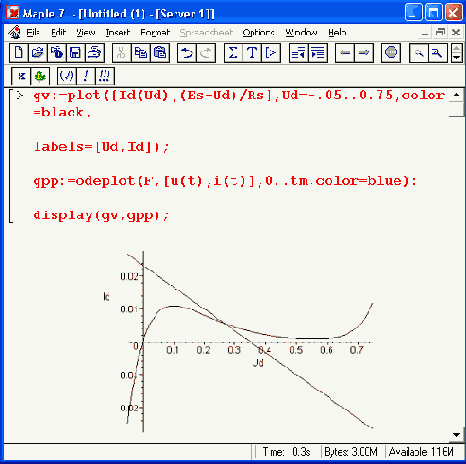
О том, что колебания релаксационные можно судить по тому, что уже первый цикл колебаний вырождается в замкнутую кривую — предельный цикл, форма которого заметно отличается от эллиптической.
Итак, мы видим, что данная цепь выполняет функцию генератора незатухающих релаксационных колебаний. Хотя поставленная задача моделирования цепи на туннельном диоде успешно решена, в ходе ее решения мы столкнулись с проблемой обеспечения малого шага по времени при решении системы дифференциальных уравнений, описывающих работу цепи. При неудачном выборе шага можно наблюдать явную неустойчивость решения.
 |
 |
 |
Моделирование рассеивания альфа- частиц
Одним из фундаментальных доказательств существования ядра у атомов стал опыт с бомбардировкой тонкой фольги из металла альфа- частицами с высокой энергией. Если бы «массивных» ядер не существовало, то альфа- частицы должны были бы спокойно пролетать сквозь тонкую фольгу, практически не отклоняясь. Однако, как физики и ожидали, некоторая часть частиц испытывала сильное отклонение и даже поворачивала назад. Очевидно, что имели место отскоки (упругие столкновения) с малыми, но массивными ядрами металла фольги.
В нашем распоряжении, увы (а может быть и к счастью), нет ускорителя альфа- частиц. Так что мы, не опасаясь облучения и очередной Чернобыльской катастрофы, сможем смоделировать это интереснейшее физическое явление с помощью математической системы Maple 7. Причем спокойно сидя перед своим домашним компьютером и глубокомысленно наблюдая за траекториями полета альфа- частиц.
Итак, пусть в нашем теоретическом опыте альфа- частицы с энергией 4 МэВ рассеиваются тонкой золотой фольгой. Рассчитать траекторию частицы, приближающейся к ядру атома Аи. Прицельное расстояние р равно 2*10-15 м. Приступим к решению задачи и зададим вначале систему дифференциальных уравнений для траектории альфа- частицы:
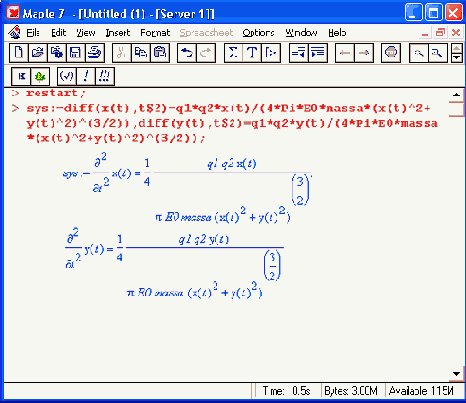
Введем исходные числовые данные для вычислений:
> ql:=2*i;6e-19:q2:=79*1.6e-19:massa:=4*1.67e-27:EO:=8.85e-12: a:=4e-13:
p:=5e-15:T:=4e6*1.6e-19:V0x:=sqrt(2*T/massa):
Создадим графическую структуру решения нашей системы дифференциальных уравнений для нескольких расчетных отклонений линии движения альфа- частицы от центра ядра атома, находящегося на ее пути:
> with(DEtools):ss:=DEplot({sys},{y(t),x(t)},t=0..7e-20.
[[x(0)=-a,D(x)(0)=VOx,y(0)=p,D(y)(0)=0].
[x(0)=-a,D(x)(0)=VOx,y(0)=p*4.D(y)(0)=0],
[x(0)=-a,D(x)(0)=VOx,y(0)=p*8,D(y)(0)=0],
[x(0)=-a,D(x)(0)=VOx,y(0)=p*12,D(y)(0)=0].
[x(0)=-a;D(x)(0)=VOx,y(0)=p*16,D(y)(0)=0],
[x(0)-a.D(x)(0)-VOx.y(0)-p*20,D(y)(0)-0].
[x(0)=-a,D(x)(0)=VOx,y(0)=p*24,D(y)(0)=0],
[x(0)=-a,D(x)(0)=VOx,y(0)=p*28,D(y)(0)=0]],
x(t)=-a..a,scene=[x(t),y(t)],stepsize=le-21,1inecolor=bl ack):
> with(plottools):yy:=circle([0.0],2E-14,color=red,thickness=2):
Warning, the name translate has been redefined
Построим центр ядра (кружок со знаком +) и траектории альфа- частиц:
> ss2:=PLOT(TEXT([0.-0.3e-14],'+'), FONT(HELVETICA, OBLIQUE.14)):
Осталось построить график траекторий движения альфа- частиц вблизи центра атома: i
> with(plots):
Warning, the name changecoords has been redefined
> disp1ay([ss,yy,ss2],tit1e='Pacceивание а-частиц',axes=framed);
График траекторий движения альфа- частиц вблизи ядра представлен на рис. 17.11. Этот график настолько нагляден, что не требует пояснения.
Моделирование движения альфа- частиц вблизи малого и «массивного» ядра атома дает наглядное представление о математической и физической сути данного опыта. Надо лишь помнить, что нельзя нацеливать альфа- частицы прямо в центр ядра. Более сложные, чем приведенные, расчеты показывают, что при этом альфа-частица настолько близко подходит к ядру, что надо учитывать новые факторы, возникающие при близком взаимодействии. Они могут привести к тому, что частица будет поглощена ядром- Но это уже тема нового разговора,, выходящего за рамки данной книги.
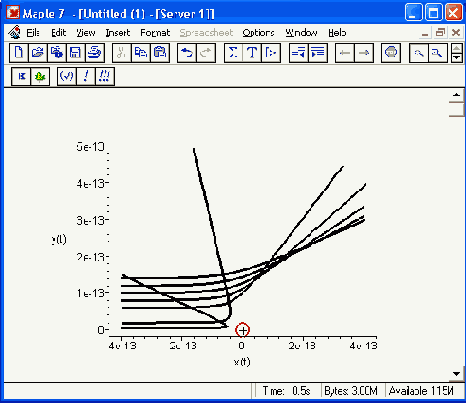
 |
 |
 |
Небольшое введение
Выше при изложении данного учебного курса приводились многие сотни примеров применения системы Maple 7. При этом намеренно подбирались достаточно простые примеры, занимающие немного места и не требующие чрезмерных ухищрений для решения.
Многие читатели полагают, что системы компьютерной математики хорошо работают на таких простых примерах, но от них мало толку при решении реальных задач математики, физики или радиоэлектроники. Это, конечно, заблуждение. Дело просто в том, что при решении таких задач руководящая роль пользователя сильно возрастает. Вы должны понимать, что не Maple 7 решает вашу задачу, а вы! И система Maple 7 лишь помогает в этом трудном деле. Так что при неудачах в решении своих специфических задач следует прежде всего пенять на себя и на свое незнание возможностей системы Maple 7, а вовсе не на свою помощницу.
В том, что Maple можно успешно использовать при решении вполне конкретных научных и практических задач, призваны убедить примеры, приведенные ниже. Разумеется, и их нельзя отнести к таким сложнейшим задачам, как проектирование ядерного реактора или расчет траектории полета космического корабля, — не стоит забывать, что такие расчеты делают на суперкомпьютерах, а не на домашнем компьютере, который стоит перед вами. И объем материалов по сопровождению и результатам таких расчетов многократно превосходит объем всей этой книги. Тем не менее в этом уроке вы встретите решение вполне реальных и полезных задач в области математики, физики и радиоэлектроники. Почему не в механике, гидродинамике или в оптике? Да потому, как верно сказал наш народный пророк Козьма Прутков: «нельзя объять необъятное». Приведенные примеры отчасти обусловлены личными пристрастиями автора, но они полезны каждому пользователю, желающему всерьез оценить возможности Maple 7.
Описанные в этом уроке задачи являются реальными документами, созданными и отлаженными в среде Maple 7 и лишь затем перенесенными в рукопись книги. Так что они заодно служат примерами того, как надо оформлять такие документы. В то же время от некоторых «излишеств» оформления (например, закрывающихся и открывающихся секций) мы отказались, дабы не усложнять описание документов явно второстепенными деталями. Начнем этот урок с решения весьма актуальной для многих областей применения математики задачи — аппроксимации сложной функции.
 |
 |
Нужно ли применять Maple для моделирования и расчета электронных схем?
Нужно ли применять системы компьютерной математики для анализа, расчета и моделирования электронных схем? Ответ на этот вопрос не так прост, как кажется с первого взгляда. С одной стороны, к услугам пользователя компьютера сейчас имеется ряд программ схемотехнического моделирования, например Micro-CAP, Electronics Workbench, PSpice, Design Labs и др., автоматически составляющих и решающих большие системы уравнений состояния электронных схем и моделирующих работу бесчисленного множества электронных схем без кропотливого «ручного» составления уравнений.
Но, с другой стороны, анализ схем в таких программах настолько автоматизирован, что начисто теряется его физическая и математическая сущность. Это не так уж страшно, когда моделируются типовые схемы на давно известных или, скорее, просто хорошо знакомых электронных приборах. Но это явно плохо, когда объектом исследования и моделирования являются новые нетрадиционные схемы на новых или малоизвестных приборах или когда знание физических и математических основ работы таких схем принципиально необходимо. Например, при изучении их в вузах и университетах. В этом случае применение систем компьютерной математики не только возможно, но и принципиально необходимо.
Паде-аппроксимация
Теперь опробуем рациональную аппроксимацию Паде (Fade) функции f(x) степени (4,4). Приближения по этому разложению будут аппроксимировать функцию более точно, и потому ошибки округления в вычислениях станут более заметными. Поэтому зададим еще два дополнительных знака для точности вычислений.
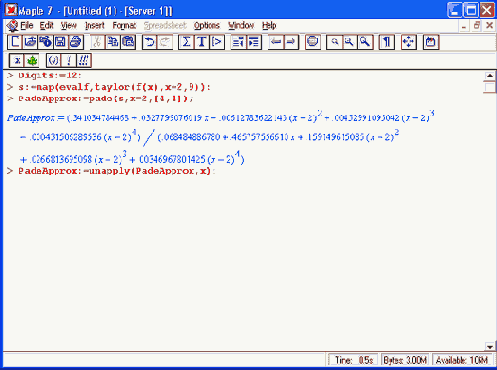
Кривая ошибки для интервала [0, 4] строится командой:

и имеет вид, показанный на рис. 17.3.
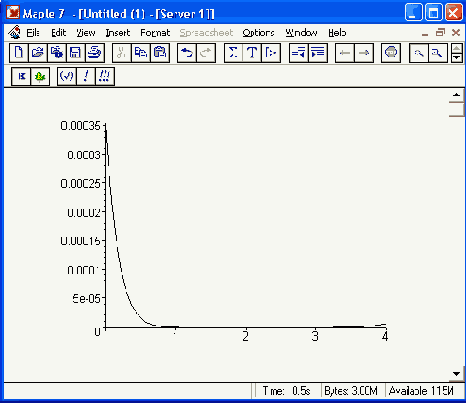
Рис. 17.3. Кривая погрешности при Паде- аппроксимации степени (4,4)
Как и при аппроксимации рядом Тейлора, ошибка здесь мала вблизи точки разложения и велика вдали от нее. Мы снова видим из графика, что для указанной функции, самая большая ошибка — в левой оконечной точке. Однако максимальная ошибка в Паде- аппроксимации уже на порядок меньше, чем при аппроксимации полиномом Тейлора:
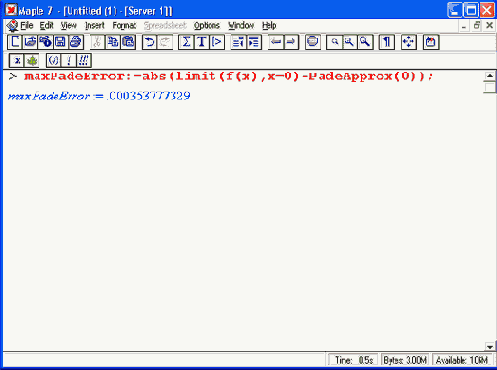
Это успех, показывающий, что мы на верном пути. Но пока погрешность остается слишком большой по сравнению с заданной.
Преобразование в код Фортрана или С
Один из поводов разработки эффективной аппроксимации для вычисления математической функции заключается в создании библиотек подпрограмм для популярных языков программирования высокого уровня, таких как Фортран или С. В Maple имеются функции преобразования на любой из этих языков. Например, мы можем преобразовывать формулу для минимаксной аппроксимации в код Фортрана.
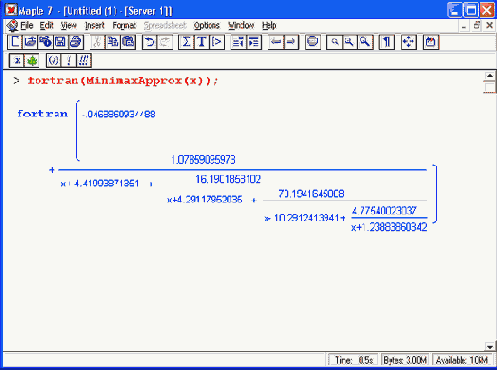
Итак, нами показано, что правильный выбор аппроксимации для сложной функции обеспечивает уменьшение времени ее вычисления более чем на два порядка (!) при весьма приличной точности в б верных знаков и при использовании для вычислений минимального числа арифметических операций. Применение при этом средств системы Maple 7 позволяет генерировать разложения в различные ряды, быстро вычислять рациональные аппроксимации функций и выполнять преобразования в различные специальные формы, сочетая это с мощными средствами интерактивной работы и графической визуализации, в частности с построением графиков функции и кривых ошибок при разных видах аппроксимации. Все это обеспечивает идеальную среду для решения таких задач.
Применение интеграла Дюамеля для расчета переходных процессов
Вернемся к линейным цепям и рассмотрим еще один полезный метод расчета электрических цепей — с помощью интеграла Дюамеля. При нем можно рассчитать временную зависимость выходного напряжения u2(t) цепи по известному входному сигналу ul(t) и переходной характеристике цепи a(t). Возьмем в качестве первого классического примера дифференцирующую RC-цепь и вычислим ее реакцию на экспоненциально нарастающий перепад напряжения.
Представлены заданные зависимости ul(t) и a(t), аналитическое выражение для интеграла Дюамеля (одна из 4 форм) и аналитическое выражение для искомой зависимости u2(t). Пока последнее выражение довольно простое. В конце этого фрагмента документа построены графики зависимостей ul(t), a(t) и u2(t).
Обратите внимание на то, что выражение для u2(t), получаемое с помощью интеграла Дюамеля, стало намного сложнее. Тем не менее получено как аналитическое выражение для реакции цепи u2(t), так и графики ul(t), a(t) и u2(t). Они показаны внизу графика.
Проектирование цифрового фильтра
Основной недостаток аналоговых активных фильтров, подобных описанному выше, заключается в их малом порядке. Его повышение за счет применения многих звеньев низкого порядка ведет к значительному повышению габаритов фильтров и их стоимости. От этого недостатка свободны современные цифровые фильтры, число ячеек которых N даже при однокристальном исполнении может достигать десятков и сотен. Это обеспечивает повышенную частотную селекцию.
Спроектируем фильтр N+1-ro порядка класса FIR (Finite Impulse Response или с конечной импульсной характеристикой). Каждая из N ячеек временной задержки фильтра удовлетворяет следующей зависимости выходного сигнала у от входного х вида:

Подключим пакет расширения plots, нужный для графической визуализации проектирования:
> restart:with(p1ots):
Warning, the name changecoords has been redefined
Зададим исходные данные для проектирования полосового цифрового фильтра, выделяющего пятую гармонику из входного сигнала в виде зашумленного меандра с частотой 500 Гц:
> N := 64: # Число секций фильтра (на 1 меньше порядка фильтра)
> fs:= 10000: # Частота квантования
> fl = 2300: # Нижняя граничная частота
> fh = 2700: # Верхняя граничная частота
> m := 10: # 2^m > N - число точек для анализа
Вычислим:

Вычислим FIR-коэффициенты для прямоугольного окна фильтра:
> С :-=(n) -> limit(g,t=n):h := aray(0..N): N2:=N/2:
> for n from 0 to N2 do h[N2-n]:= evalf(C(n)); h[N2+n] := h[N2-n]; od:
Определим массивы входного x(n) и выходного у(n) сигналов:
> х := array(-N..T): y := аггау(0..Т):
Установим значение х(n) равным 0 для времени меньше 0 и 1 для времени >=0:
> for n from -N to -1 do x[n] := 0; od:
> for n from 0 to Т do x[n] := Dirac(n); od:
Вычислим временную зависимость для выходного сигнала:
> for n from 0 to Т do y[n] := sum(h[k]*x[n-k],k=0..N): od:
Построим график импульсной характеристики фильтра, отражающей его реакцию на сигнал единичной площади с бесконечно малым временем действия:
> р := [seq([j/fs,y[j]],j=0..T)3:
> plot(p, time=0..3*N/fs, labels=[time,output], axes=boxed, xtickmarks=4, title-'Иипульсная характеристика фильтра',color=black);
Он показан на рис. 17.19. Нетрудно заметить, что эта характеристика свидетельствует об узкополосности фильтра, поскольку его частоты fl и fh различаются несильно. В этом случае полосовой фильтр по своим свойствам приближается к резонансному, хотя само по себе явление резонанса не используется.
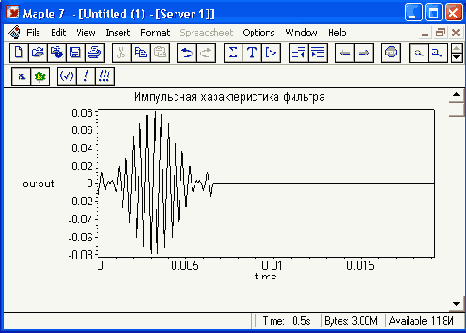
Вычислим АЧХ фильтра, используя прямое преобразование Фурье. Оно после подготовки обрабатываемых массивов реализуется функцией FFT:
> rо := array (1..T+1): io := arrayd. .T+l):
> for n from 0 to Т do ro[n+l] :- y[n]; io[n+l] := 0; od:
> FFT(m,ro,io):
Построим график АЧХ фильтра:
> р :=[seq([j*fs/(T+l),abs(ro[j+l]+io[j+l]*I)3,j=O..T/2)]:
> plot(p, frequency=0..fs/2, tabels=[frequency,gain], tit1e='AЧX фильтра',со1ог=black);
Он представлен на рис. 17.20. Нетрудно заметить, что и впрямь АЧХ фильтра напоминает АЧХ резонансной цепи — она имеет вид узкого пика. Вы можете легко проверить, что раздвижением частот fl и fh можно получить АЧХ с довольно плоской вершиной и резкими спадами (говорят, что такая характеристика приближается к прямоугольной).
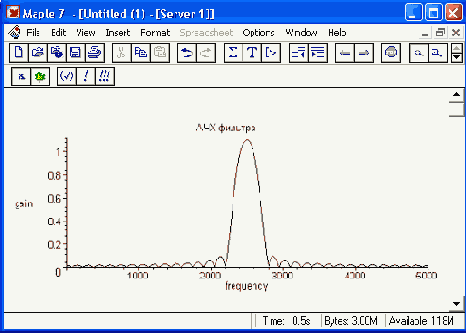
Теперь приступим к тестированию фильтра. Зададим входной сигнал в виде зашумленного меандра с частотой 500 Гц и размахом напряжения 2 В:
> 1 :=round(fs/2/500):
> for n from 0 by 2*1 to Т do
> for n2 from 0 to 1-1 do
> if n+n2 <= Т then
> x[n+n2] := evalf(-l+rand()/10^12-0.5);
> fi:
> if n+n2+1 <= Т then
> x[n+n2-H] :-=eva1f(l+ranoX)/10^12-0.5);
> fi;
> od:
> od:
Временная зависимость синтезированного входного сигнала представлена на рис. 17.21.
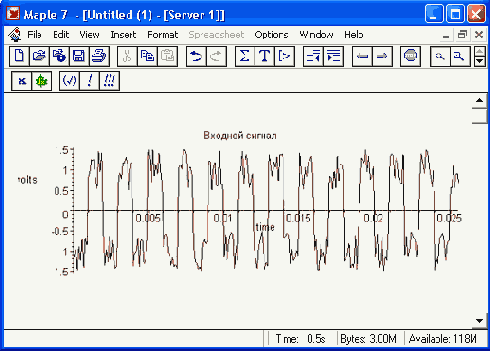
Вычислим реакцию фильтра на входной сигнал:
> for n from 0 to T do
> y[n] := sum(h[k]*x[n-k],k=0..N);
> od:
Построим график выходного сигнала:
> р := [seq([j/fs, x[j]], j=0..T)]:q:= [seq([j/fs , y[j]] , j =0..Т)]:
> plot(p,time=0..T/fs/4,1abels=[time,volts],title='Входной сигнал\сolor=black);
> plot(q,tine=0..T/fs/4,1abels=[tirae,volts], titlе='Выходной сигнал",color=black);
Временная зависимость выходного сигнала показана на рис. 17.22. Нетрудно заметить, что в конце концов выходной сигнал вырождается в пятую гармонику входного сигнала, но этому предшествует довольно заметный переходной процесс. Он связан с узкополосностью данного фильтра.

Вычислим спектры входного и выходного сигналов, подготовив массивы выборок сигналов и применив прямое преобразование Фурье с помощью функции FFT:
> Н := array(l..T+l):1i :=array(1..Т+1):
> for n from 0 to T do ,
> ri[n+l] := x[n]*2/T: ii[rn-l] := 0;
> ro[n+l] := y[n]*2/T; Io[rrfl] := 0;
> od:
> FFT(m.ri,ii):rTT(m,ro,io):
Построим график спектра входного сигнала, ограничив масштаб по амплитуде значением 0,5 В:
> р := [seq([j*fs/(T+l),abs(n[j+l]+ii[j-H]*I)],j=0..T/2)]:
> q := [seq([j*fs/(T-H),abs(ro[j-H]+To[j+l]*I)],j=0..T/2)]:
> plot(p, frequency=0..fs/2,y0..0.5,labe1s=[Частотa.V],title='Частотный спектр входного сигнала',color=black);
Этот график представлен на рис. 17.23. Из него хорошо видно, что спектральный состав входного сигнала представлен только нечетными гармониками, амплитуда которых убывает по мере роста номера гармоники. Пятая гармоника на частоте 2500 Гц находится посередине полосы пропускания фильтра, ограниченной граничными частотами фильтра 2300 и 2700 Гц. Заметны также беспорядочные спектральные линии шума сигнала в пределах полосы прозрачности фильтра.
Теперь построим график спектра выходного сигнала:
> p1ot(q, frequency=0..fs/2,y=0..0.5,labe1s=[Частотa,V], title='Частотный спектр выходного сигнала'бcolor=black);
Он представлен на рис.17.24. Хорошо видно эффективное выделение пятой гармоники сигнала и прилегающей к ней узкой полосы шумового спектра.
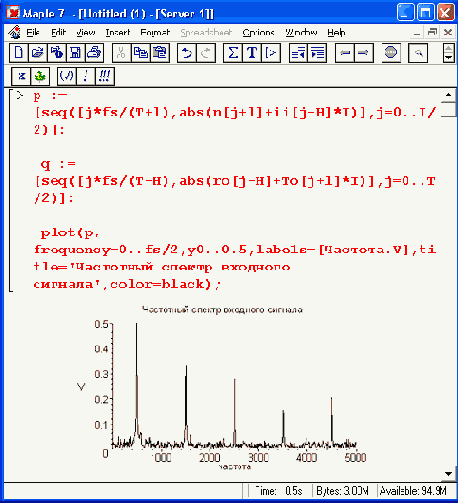

Приведенные данные свидетельствуют, что спроектированный фильтр полностью отвечает заданным требованиям и обеспечивает уверенное выделение пятой гармоники зашумленного меандра. По образу и подобию данного документа можно выполнить проектирование и других видов цифровых фильтров.
 |
 |
 |
Расчет аналогового фильтра на операционном усилителе
Теперь рассмотрим проектирование аналогового полосового фильтра на операционном усилителе, схема которого приведена на рис. 17.16.

Рис. 17.16. Схема полосового фильтра на интегральном операционном усилителе
Подготовимся к расчету фильтра:
> restart:
Зададим основные уравнения, описывающие работу фильтра на малом сигнале:
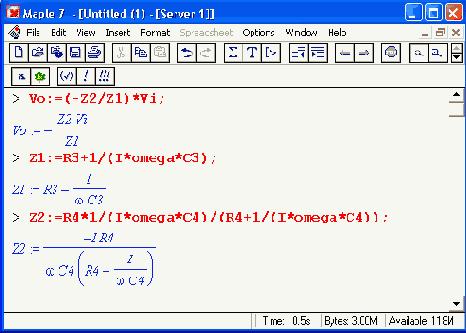
Введем круговую частоту:
> omega := 2*Pi*f;
W := 2пf
Найдем коэффициент передачи фильтра и его фазо-частотную характеристику как функции от частоты:
> gain := abs(eva1c(Vo/Vi)):
> phase := evalc(op(2,convert(Vo/Vi.polar))):
Для просмотра громоздких аналитических выражений для этих параметров замените знаки двоеточия у выражений для gain и phase на знак точки с запятой. Далее введем конкретные исходные данные для расчета:
> R3 :=1000:
> R4 := 3000:
> СЗ :=0.08*10^(-6):
> С4 := 0.01*10^(-6):
Построим АЧХ фильтра как зависимость коэффициента передачи в децибелах (dB) от частоты f в Гц:
> plot(DogWf), 20*log10(gain), f=[10..50000], color=black, title='Коэффициент передачи dB как функция от частоты f в Гц'):
Эта характеристика представлена на рис. 17.17. Здесь полезно обратить внимание на то, что спад усиления на низких и высоких частотах происходит довольно медленно из-за малого порядка фильтра.
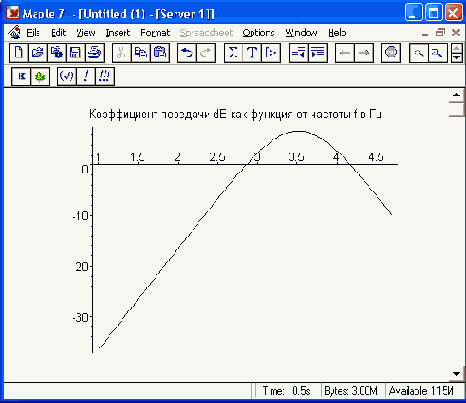
Рис. 17.17. АЧХ фильтра на операционной усилителе
Далее построим фазо-частотную характеристику фильтра как зависимость фазы в радианах от частоты f в Гц:
> plot ([log10(f),phase, f=10..50000], color=black, title=*Фазо-частотная характеристика фильтра*);
Фазо-частотная характеристика (ФЧХ) фильтра показана на рис. 17.18
На ФЧХ фильтра можно заметить характерный разрыв, связанный с превышением фазовым углом граничного значения я. Такой способ представления фазового сдвига общепринят, поскольку его изменения стремятся вписать в диапазон от -я до п.
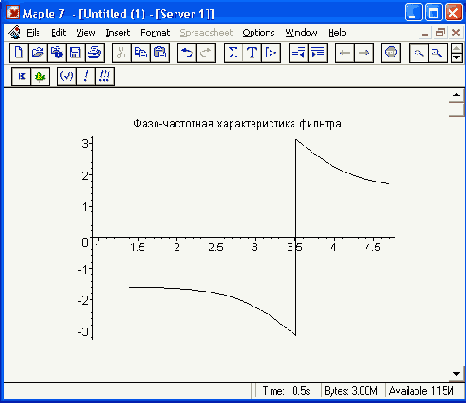
Рис. 17.18. ФЧХ фильтра на операционном усилителе
Расчет траектории камня с учетом сопротивления воздуха
Вы хотите метнуть камень в огород вашего вредного соседа? Разумеется, во время его отсутствия. Давайте промоделируем эту ситуацию, предположив два актуальных случая: дело происходит на Луне и на Земле. В первом случае сопротивления воздуха (как и его самого) нет, а в другом — сопротивление воздуха есть и его надо учитывать. Иначе камень упадет в ваш огород, а не в огород соседа!
Итак, пусть подвернувшиеся под руку камни с массой 500 и 100 г брошены под углом 45° к горизонту со скоростью Vo = 20 м/с. Найдем их баллистические траектории, если сила сопротивления воздуха Fтр=А*V, где А=0,1 Н*с/м. Сравним их с траекториями, получающимися без учета сопротивления воздуха.
Начнем с подключения пакета plots, нужного для визуализации данной задачи:
> restart;
> with(plots):
Warning, the name changecoords has been redefined
Составим параметрические уравнения для проекций скорости на оси координат:
> Vox:=Vo*cos(a1pha):Voy:=Vo*sin(alpha):
Vox:= Focos(a)
Voy :=Vo sin(a)
Мы рассматриваем два случая: камень массой 500 г и камень массой 100 г. Поскольку для каждого случая мы предусматриваем расчет в двух вариантах (с учетом сопротивления воздуха и без такого учета), то мы должны составить 4 системы дифференциальных уравнений (ДУ). Каждая система состоит из двух ДУ второго порядка и вид этих систем известен из курса физики. Ниже представлено задание этих систем ДУ (для первой системы дан вывод ее вида):
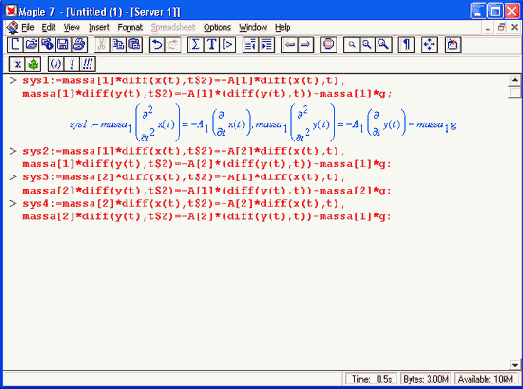
Зададим исходные числовые безразмерные данные для расчета:

Выполним решение заданных систем ДУ:
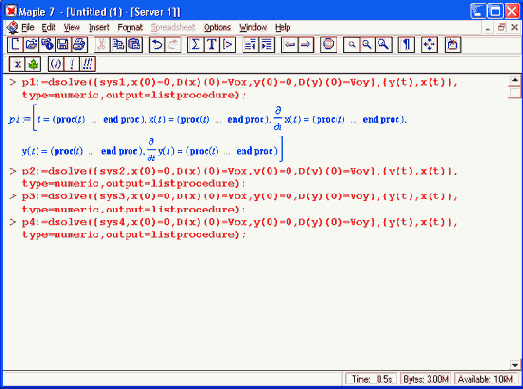
Создадим графические объекты — результаты решения систем ДУ:
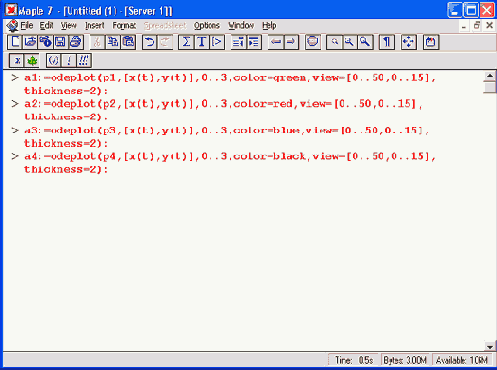
Построим графики траекторий для первого случая:
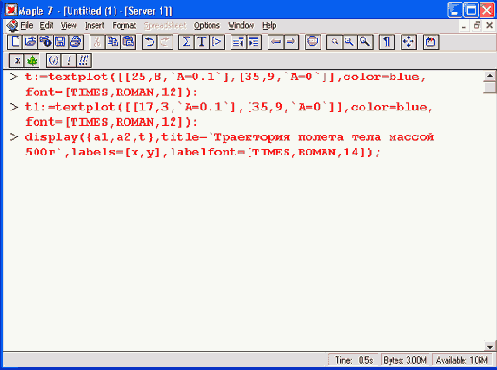
Графики траекторий полета камня с массой 500 г представлены на рис. 17.6.
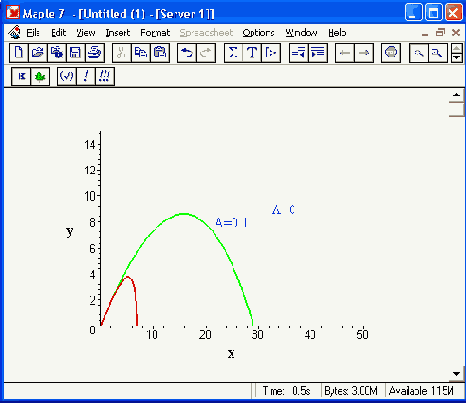
Рис. 17.6. Баллистические траектории камня с массой 500 г
Теперь построим графики траекторий для второго случая:
> display({a3,a4,t1},title='Tpaeкт. полета тела массой 100 г, labels=[x.у], labelfont=[TIMES.ROMAN,14]):
Они представлены на рис. 17.7.
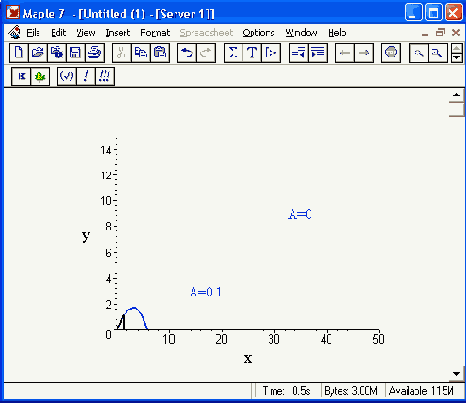
Рис. 17.7. Баллистические траектории камня при массе 100 г
Из проведенных расчетов и графиков видно, что при учете силы сопротивления воздуха дальность и высота полета сильно уменьшаются по сравнению с полетом в вакууме, и эта разница зависит от массы тела, поэтому при небольшой массе тела сопротивлением воздуха пренебрегать нельзя.
Разделение изотопов
Рассмотрим еще одну классическую задачу ядерной физики — разделение изотопов (атомов с одинаковым зарядом ядра, но разной массой). Для этого используют различные способы. В частности, это может быть масс-спектроскопический метод. Из точки А вылетают однозарядные ионы (q = е = 1.6*10-19 Кл) разной массы (от 20 до 23 а.е.м.) и под разными углами в пределах от 80 до 100° к оси х в плоскости ху (рис. 17.9). Вдоль оси z приложено магнитное поле В=10-2 Тл. Рассчитаем траектории полета частиц. Будем надеяться, что это подскажет способ разделения изотопов.
Приступим к решению данной задачи. Сила Лоренца, действующая на движущуюся частицу, F = q*(E+[v, В]). Проекции векторного произведения [v, В] на оси х, у, z заданы выражениями:
[v.B]x-vy*Bz-vz*By [v,B]y-vz*Bx-vx*Bz [v,B]z=vx*By-vy*Bz
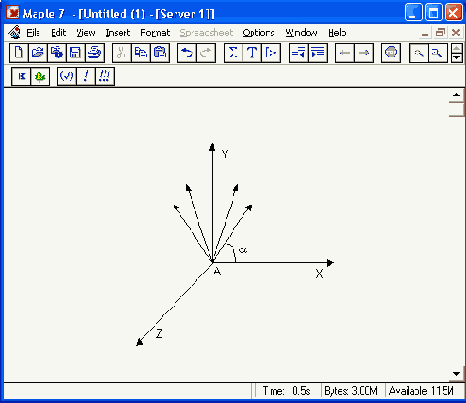
Рис. 17.9. Иллюстрация к методу разделения изотопов
В соответствии с этим дифференциальные уравнения, описывающие траекторию полета частицы по осям х, у, z имеют вид:
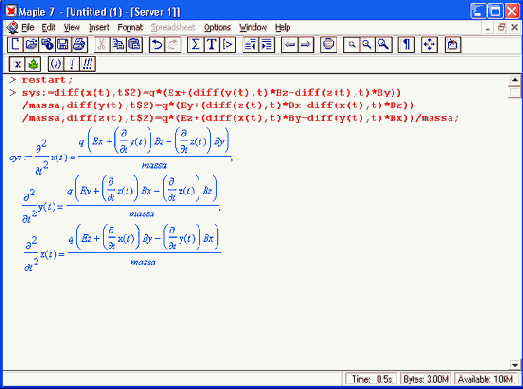
Зададим исходные числовые данные для расчета:
> q:=1.6e-19:V:=le4:
> Vx:=V*cos(a1pha):Vy:=V*sin(a1pha):Ex:=0:Ey:=0:Ez:=0:Bx:=0: By:=0:Bz:=le-2:
Выполним решение составленной выше системы дифференциальных уравнений:

Построим графики решения:
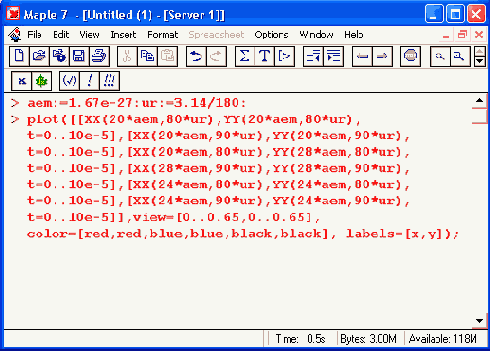
Эти графики показаны на рис. 17.10.

Рис. 17.10. Траектории движения частиц
Полученные графики (рис. 17.10) наглядно показывают на одну из возможностей разделения изотопов. Как говорится, осталось подставить «стаканчик» в нужное место для ловли нужных изотопов. Разумеется, это только изложение идеи одного из методов разделения изотопов. Увы, на практике приходится использовать сложнейшие и дорогие физические установки для решения этой актуальной задачи.
Сравнение времен вычислений
Теперь определим время, необходимое для вычисления функции/(л:) в 1000 точек, используя первоначальное интегральное определение, и сравним его с временем, требующимся для схемы MinimaxApprox в виде непрерывной дроби. Так как наше приближение будет давать только 6 точных цифр, мы также потребуем 6 точных цифр и от интегрального представления функции:
> Digits :=б: St :=time():
> seq( evalf(f(i/250.0)), i = 1..1000 ):
> oldtime := time() - st;
oldtime-81.805
В процессе вычислений с использованием представления рациональной функции в виде непрерывной дроби иногда требуется внести несколько дополнительных цифр точности для страховки. В данном случае достаточно внести две дополнительные цифры. Итак, новое время вычислений:
> Digits := 8: st := tirae():
> seq( MinimaxApprox(i/250.0), i = 1..1000 ):
> newtime :» time()- st;
newtime:= .694
Ускорение вычисления при аппроксимации есть:
> SpeedUp := oldtime/newtime;
SpeedUp:=U7.S7464
Мы видим, что процедура вычислений, основанная на MinimaxApprox, выполняется почти в 120 раз быстрее процедуры с использованием исходного интегрального определения. Это просто феноменальный успех, полностью оправдывающий время, потерянное на предварительные эксперименты по аппроксимации и ее оптимизации! Разумеется, при условии, что вы будете применять эту аппроксимацию многократно.
Задание исходной функции и построение ее графика
Трудно представить себе область более широкую и>й6читаемую, чем аппроксимация различных функциональных зависимостей. С получения простой аппроксимации сложной зависимости нередко начинаются (а часто и заканчиваются) научные исследования во многих областях как прикладной, так и фундаментальной науки. Покажем возможности в этом системы Maple 7 на одном из примеров, давно помещенных в библиотеку пользователей системы Maple V R2, и переработанных для Maple 7.
Воспользуемся возможностями пакета numapprox, для чего прежде всего подключим его:
> restart:with(numapprox):
[chebdeg,chebmult,chebpade,chebsort,chebyshev, confracform,hermite_pade,hornerform, infnorm,laurent,minimax,pade,remez]
Будем искать приемлемую аппроксимацию для следующей, отнюдь не простой, тестовой функции:
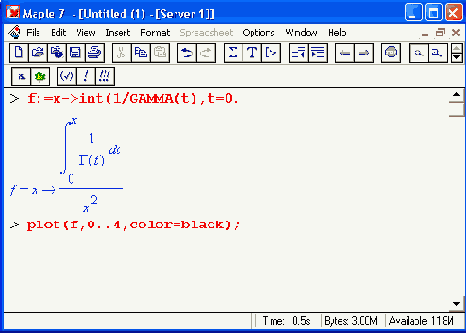
График этой функции представлен на рис. 17.1. С первого взгляда — это простой график, но тут как раз тот случай, когда простота обманчива. Вы сразу Заметите, что график строится необычно медленно, поскольку в каждой из множества его точек системе Maple 7 приходится вычислять значение интеграла с подынтегральной функцией, содержащей довольно каверзную гамма- функцию. И делает это Maple 7 по сложному и медленному алгоритму адаптивного численного интегрирования.
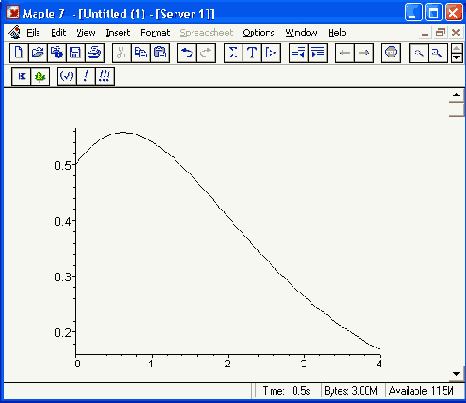
Рис. 17.1. График аппроксимируемой функции
Итак, вычисление f(x) по ее интегральному представлению совершенно не эффективно. Наша цель состоит в разработке процедуры вычислений, которая дала бы 6 точных цифр результата в интервале [0..4] и требовала, по возможности, наименьшего числа арифметических операций для каждого вычисления. Втайне не вредно помечтать о том, чтобы после аппроксимации время вычислений уменьшилось бы хотя в несколько раз. Что получится на деле, вы увидите чуть позже. А пока войдем в дебри аппроксимации.
